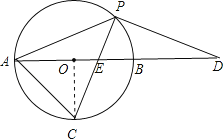
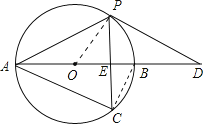
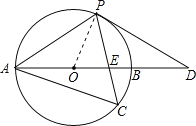
【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.

(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若![]() :
:![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CE![]() CP的值.
CP的值.
参考答案:
【答案】(1)PD与⊙O相切.理由见解析;(2)3:1:2(3)8
【解析】
试题分析:(1)连OP,根据圆周角定理得到∠AOP=2∠ACP=120°,则∠PAO=∠APO=30°,利用PA=PD得到∠D=∠PAD=30°,则∠APD=180°﹣30°﹣30°=120°,于是得到∠OPD=120°﹣30°=90°,根据切线的判定定理即可得到PD是⊙O的切线;
(2)连BC,由AB为直径,根据直径所对的圆周角为直角得到∠ACB=90°,利用![]() :
:![]() =1:2,则∠ABC=2∠BAC,所以有∠BAC=30°,∠ABC=60°,而∠PAE=30°,得到AE垂直平分PC,设BE=x,然后利用含30°的直角三角形三边的关系可求出AE:EB:BD的值;
=1:2,则∠ABC=2∠BAC,所以有∠BAC=30°,∠ABC=60°,而∠PAE=30°,得到AE垂直平分PC,设BE=x,然后利用含30°的直角三角形三边的关系可求出AE:EB:BD的值;
(3)根据圆周角定理由弧AC=弧BC,得到∠CAB=∠APC,OC⊥AB,根据相似三角形的判定方法易得△ACE∽△PCA,则![]() ,即AC2=PC
,即AC2=PC![]() CE,利用勾股定理有A02+OC2=AC2=8,即可得到CE
CE,利用勾股定理有A02+OC2=AC2=8,即可得到CE![]() CP的值.
CP的值.
解:(1)PD与⊙O相切.理由如下:
连接OP,
∵∠ACP=60°,
∴∠AOP=120°,
而OA=OP,
∴∠PAO=∠APO=30°,
∵PA=PD,
∴∠D=∠PAD=30°,
∴∠APD=180°﹣30°﹣30°=120°,
∴∠OPD=120°﹣30°=90°,
∵OP为半径,
∴PD是⊙O的切线;
(2)连BC,
∵AB为直径,
∴∠ACB=90°,
∵![]() :
:![]() =1:2,
=1:2,
∴∠ABC=2∠BAC,
∴∠BAC=30°,∠ABC=60°,
而∠PAE=30°,
∴∠APE=∠DPE=60°,
∴AE垂直平分PC,如图,
设BE=x,在Rt△BCE中,∠BCE=30°,则BC=2BE=2x,
在Rt△ABC中,∠CAB=30°,AB=2BC=4x,
∴AE=AB﹣BE=3x,
∵PA=PD,PE⊥AD,
∴AE=DE,
∴DB=3x﹣x=2x,
∴AE:EB:BD的值为3:1:2;
(3)如图,连接OC,
∵弧AC=弧BC,CO⊥AD,
∴∠CAB=∠APC,OC⊥AB,
而∠ACE=∠PCA,
∴△ACE∽△PCA,
∴![]() ,即AC2=PC
,即AC2=PC![]() CE,
CE,
∵A02+OC2=AC2=8,
∴PC![]() CE=AC2=8.
CE=AC2=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式(m+1)(m﹣1)+(m+1)提取公因式m+1后,余下的部分是( )
A. m+1B. m﹣1C. mD. 2 m+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】将12000000用科学计数法表示是 ( )
A. 12×106 B. 120×105 C. 0.12×108 D. 1.2×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y=
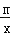 的图象经过点A.
的图象经过点A.
(1)点E的坐标是 ;
(2)求反比例函数的解析式;
(3)求当一次函数的值小于反比例函数的值时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )
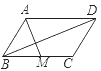
A.30 B.36 C.54 D.72
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
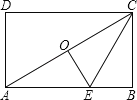
A.
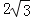 B.
B.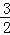
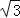 C.
C.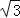 D.6
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B100的坐标为 .

相关试题

