【题目】已知:关于x的一元二次方程mx2﹣(3m+2)x+2m+2=0(m>0)
(1)求证:方程有两个不相等的实数根且其中一根为定值.
(2)设方程的两个实数根分别为x1 , x2(其中x1<x2).若y是关于m的函数,且y=7x1﹣mx2 , 求这个函数的解析式;并求当自变量m的取值范围满足什么条件时,y≤3m.
参考答案:
【答案】
(1)证明:△=(3m+2)2﹣4m(2m+2)
=m2+4m+4
=(m+2)2,
∵m>0,
∴(m+2)2>0,即△>0,
∴方程有两个不相等的实数根,
∵x= ![]() ,
,
∴方程有一个根为1,
∴方程有两个不相等的实数根且其中一根为定值
(2)解:∵x= ![]() ,
,
∴x1=1,x2=2+ ![]() ,
,
∴y=7x1﹣mx2
=7﹣m(2+ ![]() )
)
=﹣2m+5,
当y≤3m,即﹣2m+5≤3m,
∴m≥1
【解析】(1)先计算判别式的值得到△=(m+2)2 , 由m>0,得到△>0,根据判别式的意义得到方程有两个不相等的实数根,再利用求根公式得到x= ![]() ,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.(2)解方程得到x1=1,x2=2+
,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.(2)解方程得到x1=1,x2=2+ ![]() ,所以y=7﹣m(2+
,所以y=7﹣m(2+ ![]() )=﹣2m+5,然后解不等式﹣2m+5≤3m.
)=﹣2m+5,然后解不等式﹣2m+5≤3m.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶.他距乙地的距离y(km)与时间x(h)的关系如图中折线所示,小李开车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离y(km)与时间x(h)的关系如图中线段AB所示.

(1)小李到达甲地后,再经过_______小时小张也到达乙地;小张骑自行车的速度是_______千米/小时.
(2)小张出发几小时与小李相距15千米?
(3)若小李想在小张休息期间与他相遇,则他出发的时间x应在什么范围?(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起,催生了快递行业的高速发展.据调查,杭州市某家小型快递公司,今年一月份与三月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率;
(2)如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务?如果不能,请问至少需要增加几名业务员? -
科目: 来源: 题型:
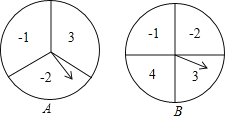
查看答案和解析>>【题目】如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b.
(1)请用列表或画树状图的方法写出所有的可能;
(2)求一次函数y=kx+b的图象经过一、二、四象限的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x+3的顶点坐标是 .
相关试题

