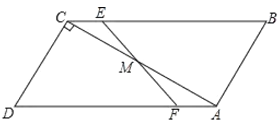
【题目】如图，已知四边形ABCD是平行四边形，AC为对角线，∠DAC=30°，∠ACD=90°，AD=8，点M为AC的中点，动点E从点C出发以每秒1个单位的速度运动到点B停止，连接EM并延长交AD于点F，设点E的运动时间为t秒．
(1)求四边形ABCD的面积；
(2)当∠EMC=90°时，判断四边形DCEF的形状，并说明理由；
(3)连接BM，点E在运动过程中是否能使△BEM为等腰三角形?如果能，求出t；如果不能，请说明理由．
【答案】（1）16
（2）菱形，理由见解析（3）t＝5.2或t＝82
时，△BEM为等腰三角形
【解析】
（1）利用直角三角形中30°角所对的直角边等于斜边的一半求得平行四边形的定和高，再利用底乘以高计算面积；
（2）结合∠EMC＝90°以及平行四边形的性质，可证明四边形DCEF是平行四边形，再通过计算得到平行四边形CDFE的一组邻边相等即可证得结论；
（3）探究△BEM为等腰三角形，要分三种情况进行讨论：EB＝EM，EB＝BM，EM＝BM．通过相应的计算表示出BE，EM，BM，然后利用边相等建立方程进行求解．
（1）∵∠DAC＝30°，∠ACD＝90°，AD＝8，
∴CD＝4，AC＝
=4．
又∵四边形ABCD为平行四边形，
∴四边形ABCD的面积为4×4＝16．
（2）如图1，当∠EMC＝90°时，四边形DCEF是菱形．
∵∠EMC＝∠ACD＝90°，
∴DC∥EF．
∵BC∥AD，
∴四边形DCEF是平行四边形，∠BCA＝∠DAC．
由（1）可知：CD＝4，AC＝4．
∵点M为AC的中点，
∴CM＝2．
在Rt△EMC中，∠CME＝90°，∠BCA＝30°．
∴CE＝2ME，可得ME2＋（2）2＝（2ME）2，
解得：ME＝2．
∴CE＝2ME＝4．
∴CE＝DC．
又∵四边形DCEF是平行四边形，
∴四边形DCEF是菱形．
（3）点E在运动过程中能使△BEM为等腰三角形．
理由：如图2，过点B作BG⊥AD与点G，过点E作EH⊥AD于点H，连接DM．
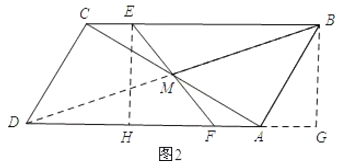
∵DC∥AB，∠ACD＝90°，
∴∠CAB＝90°．
∴∠BAG＝180°30°90°＝60°．
∴∠ABG＝30°．
∴AG＝
AB＝2，BG＝
=2
．
∵点E的运动速度为每秒1个单位，运动时间为t秒，
∴CE＝t，BE＝8t．
在△CEM和△AFM中
，
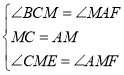∴△CEM≌△AFM．
∴ME＝MF，CE＝AF＝t．
∴HF＝HGAFAG＝BEAFAG＝8t2t＝62t．
∵EH＝BG＝2，
∴在Rt△EHF中，ME＝EF＝
＝
．
∵M为平行四边形ABCD对角线AC的中点，
∴D，M，B共线，且DM＝BM．
∵在Rt△DBG中，DG＝AD＋AG＝10，BG＝2，
∴BD=
故BM＝×4＝2．
要使△BEM为等腰三角形，应分以下三种情况：
当EB＝EM时，有(8t)2＝
[12＋(62t)2]，
解得：t＝5.2．
当EB＝BM时，有8t＝2，
解得：t＝82．
当EM＝BM时，由题意可知点E与点B重合，此时点B、E、M不构成三角形．
综上所述，当t＝5.2或t＝82时，△BEM为等腰三角形．
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】第十五届中国“西博会”已于
年
月底在成都召开，现有
名志愿者准备参加某分会场的工作，其中男生
人，女生
人．
（1）若从这人中随机选取一人作为联络员，求选到女生的概率；
（2）若该分会场的某项工作只在甲、乙两人中选一人，他们准备以游戏的方式决定由谁参加，游戏规则如下：将四张牌面数字分别为
、
、
、
的扑克牌洗匀后，数字朝下放于桌面，从中任取张，若牌面数字之和为偶数，则甲参加，否则乙参加．试问这个游戏公平吗？请用树状图或列表法说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC中，∠B=90°，AB=9,BC=12，点p从点A开始延边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P．Q分别从A．B同时出发，当点Q运动到点C时，两点停止运动，问：
（1）填空：BQ=______，PB=______（用含t的代数式表示）
（2）经过几秒，PQ的长为 
cm？
（3）经过几秒，
的面积等于
?
查看答案和解析>>
科目：初中数学 来源： 题型：
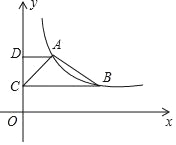
【题目】如图，在平面直角坐标系中，反比例函数y=
（x＞0，k＞0）的图象经过点A（1，a），B（m，n）（m＞0），分别过A、B两点作y轴垂线，垂足分别为D，C，且CD=
．
（1）求k关于n的关系式；
（2）当△ABC面积为2时，求反比例函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点 B、O分别落在点 B1、C1 处，点B1在x轴上，再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置，点 A2 在x轴上，依次进行下去…．若点 A（
，0），B（0，4），则点 B2016 的横坐标为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后，可以进行进一步研究，请根据示例图形，完成下表．
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| （1）__________． |
|
轴对称 |
| （2）__________． | （3）__________． |
旋转 |
|
| （4）__________． |
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB＝25km，CA＝15km，DB＝10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
