【题目】如图，点分别是轴上位于原点两侧的两点，点在第一象限，直线 交轴于点，直线交轴于点，.

(1)求;

(2)求点的坐标及的值;

(3)若，求直线的函数表达式.

参考答案：

【答案】(1) 三角形的面积为2；(2) ，；(3) .

【解析】

（1）已知P的横坐标，即可知道△OCP的边OC上的高长，利用三角形的面积公式即可求解；
（2）求得△AOC的面积，即可求得A的坐标，利用待定系数法即可求得AP的解析式，把x=2代入解析式即可求得p的值；
（3）根据S△AOP=S△BOP，可以得到OB=OA，则A的坐标可以求得，利用待定系数法即可求得BD的解析式．

(1)作PE⊥y轴于E，

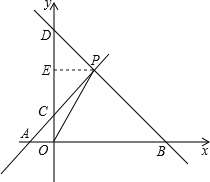
∵P的横坐标是2，则PE=2.

∴

(2)∴

∴,即

∴OA=4，

∴A的坐标是(4,0).

设直线AP的解析式是y=kx+b，则

，

解得：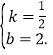

则直线的解析式是

当x=2时，y=3，即p=3；

(3)∵

∴OB=OA=4,则B的坐标是(4,0)，

设直线BD的解析式是y=mx+n，则

解得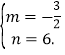

则BD的解析式是：.

关闭