【题目】△ABC中,AB=12,AC= ![]() ,∠B=30°,则△ABC的面积是 .
,∠B=30°,则△ABC的面积是 .
参考答案:
【答案】21 ![]() 或15
或15 ![]()
【解析】解:①如图1,作AD⊥BC,垂足为点D, 
在Rt△ABD中,∵AB=12、∠B=30°,
∴AD= ![]() AB=6,BD=ABcosB=12×
AB=6,BD=ABcosB=12× ![]() =6
=6 ![]() ,
,
在Rt△ACD中,CD= ![]() =
= ![]() =
= ![]() ,
,
∴BC=BD+CD=6 ![]() +
+ ![]() =7
=7 ![]() ,
,
则S△ABC= ![]() ×BC×AD=
×BC×AD= ![]() ×7
×7 ![]() ×6=21
×6=21 ![]() ;②如图2,作AD⊥BC,交BC延长线于点D,
;②如图2,作AD⊥BC,交BC延长线于点D,
由①知,AD=6、BD=6 ![]() 、CD=
、CD= ![]() ,
,
则BC=BD﹣CD=5 ![]() ,
,
∴S△ABC= ![]() ×BC×AD=
×BC×AD= ![]() ×5
×5 ![]() ×6=15
×6=15 ![]() ,
,
故答案为:21 ![]() 或15
或15 ![]() .
.
过A作AD⊥BC于D(或延长线于D),根据含30度角的直角三角形的性质得到AD的长,再根据勾股定理得到BD,CD的长,再分两种情况:如图1,当AD在△ABC内部时、如图2,当AD在△ABC外部时,进行讨论即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC的两边分别与∠DEF的两边平行,即BA∥ED,BC∥EF.

(1)在图1中,射线BA与ED同向,BC与EF也同向,∠B与∠E的数量关系是: ;
(2)在图2中,射线BA与ED异向,BC与EF也异向,∠B与∠E的数量关系是: ;
(3)在图3中,射线BA与ED同向,BC与EF异向,∠B与∠E有怎样的数量关系,并说明理由;
(4)通过上面(1)、(2)、(3),你可得到的结论是:如果一个角的两边分别平行于另一个角的两边,则这两个角的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为米. (注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12
 米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=
米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=  ,则CE的长为米.
,则CE的长为米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+(﹣7),c=(
 )÷
)÷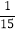 .
.(1)求2[a﹣(b+c)]﹣[b﹣(a﹣2c)]的值.
(2)若A=(﹣
 )2÷(﹣
)2÷(﹣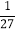 )+(1﹣
)+(1﹣ )2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
)2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB═
 cm,求BC的长.
cm,求BC的长.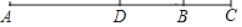
相关试题

