Question

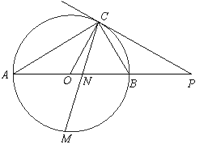
【题目】如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．

（1）求证：PC是⊙O的切线；

（2）点M是弧AB的中点，CM交AB于点N，若AB=4，求MN·MC的值．

Answer 1

【答案】（1）证明见解析；（2）8.

【解析】试题分析：（1）已知C在圆上，故只需证明OC与PC垂直即可；根据圆周角定理，易得∠PCB+∠OCB=90°，即OC⊥CP；故PC是 O的切线；（2）连接MA，MB，由圆周角定理可得∠ACM=∠BCM，进而可得△MBN∽△MCB，故BM2=MNMC；代入数据可得MNMC=BM2=8．

试题解析：(1)证明：∵OA=OC，

∴∠A=∠ACO.

又∵∠COB=2∠A，∠COB=2∠PCB，

∴∠A=∠ACO=∠PCB.

又∵AB是O的直径，

∴∠ACO+∠OCB=90°.

∴∠PCB+∠OCB=90°，OC⊥CP.

∵OC是O的半径，

∴PC是O的切线。

(2)连接MA，MB，

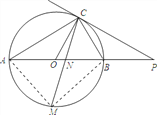
∵点M是的中点，

∴ =.

∴∠ACM=∠BCM.

∵∠ACM=∠ABM，

∴∠BCM=∠ABM.

∵∠BMN=∠BMC，

∴△MBN∽△MCB.

∴.

∴BM2=MNMC.

又∵AB是O的直径,AM=BM，

∴∠AMB=90°，AM=BM.

∵AB=4，

∴BM=.

∴MNMC=BM2=8.