【题目】某超市经销一种绿茶,每千克成本为60元,经过市场调查发现,在一段时间内,该种绿茶的销售量y(千克)与销售单价x(元)满足一次函数关系,其变化如下表所示:
销售单价(x元) | 65 | 70 | 75 | 80 |
销售量(y千克) | 110 | 100 | 90 | 80 |
(1)求y与x的函数解析式;
(2)当销售单价为多少元时,该种绿茶的销售利润最大?
(3)如果物价部门规定这种绿茶每千克销售单价不高于95元,若超市计划在这段时间内获得该种绿茶的销售利润为1 600元,其销售单价应定为多少?
参考答案:
【答案】(1) y与x的函数解析式为y=-2x+240; (2)当销售单价为90元时,该种绿茶的销售利润最大;(3)其销售单价应定为80元.
【解析】【试题分析】(1)根据表格里的数据,得该种绿茶的销售量y(千克)与销售单价x(元)满足一次函数关系,用待定系数法求一次函数的表达式,设y=kx+b,用两组数据代入,得二元方程组,求解即可.
例如,x=65时,y=110;x=70时,y=100,有![]() 解得
解得![]()
∴y与x的函数解析式为y=-2x+240;
(2)设该种绿茶的销售利润为P元,则利润等于单位数量的利润乘以销售量,即P=(x-60)y=(x-60)(-2x+240)=-2x2+360x-14400.化为顶点式,得:即P=-2(x-90)2+1800.
当x为90时,P有最大值1800.即当销售单价为90元时,该种绿茶的销售利润最大;
(3)列二元方程即可,即P=1600,则-2x2+360x-14400=1600,解得x1=80,x2=100(因为x不高于95,所以不合题意,舍去).
答:其销售单价应定为80元.
【试题解析】
(1)由该种绿茶的销售量y(千克)与销售单价x(元)满足一次函数关系,设y=kx+b,
∵x=65时,y=110;x=70时,y=100,有
![]() 解得
解得![]()
∴y与x的函数解析式为y=-2x+240;
(2)设该种绿茶的销售利润为P元,则P=(x-60)y=(x-60)(-2x+240)=-2x2+360x-14400.
即P=-2(x-90)2+1800.
∵-2<0,∴P有最大值;当x为90时,P有最大值1800.
∴当销售单价为90元时,该种绿茶的销售利润最大;
(3)令P=1600,则-2x2+360x-14400=1600,
(x-90)2=100,解得x1=80,x2=100(因为x不高于95,所以不合题意,舍去).
答:其销售单价应定为80元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,BC=5,∠B=60°,则△ABC的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是不确定事件的是( )
A. 三条线段可以组成一个三角形B. 内错角相等,两条直线平行
C. 对顶角相等D. 平行于同一条直线的两条直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角是140°,那么这个角的余角是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+
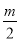 -
- =0的两个实数根.
=0的两个实数根.(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个不可能事件_____.
相关试题

