Question

【题目】如图，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF；

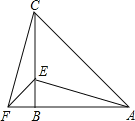
（1）求证：Rt△ABE≌Rt△CBF；

（2）求证：AB=CE+BF；

（3）若∠CAE=30°，求∠ACF度数．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）60°

【解析】

试题分析：（1）根据在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，可以得到Rt△ABE和Rt△CBF全等的条件，从而可以证明Rt△ABE≌Rt△CBF；

（2）根据Rt△ABE≌Rt△CBF，可以得到AB=BC，BE=BF，然后即可转化为AB、CE、BF的关系，从而可以证明所要证明的结论；

（3）根据Rt△ABE≌Rt△CBF，AB=CB，∠CAE=30°，可以得到∠ACF的度数．

（1）证明：∵∠ABC=90°，

∴∠ABE=∠CBF=90°，

在Rt△ABE和Rt△CBF中，

，

∴Rt△ABE≌Rt△CBF（HL）；

（2）证明：∵Rt△ABE≌Rt△CBF，

∴AB=BC，BE=BF，

∵BC=BE+CE，

∴AB=CE+BF．

（3）∵AB=CB，∠ABC=90°，∠CAE=30°，∠CAB=∠CAE+∠EAB，

∴∠BCA=∠BAC=45°，

∴∠EAB=15°，

∵Rt△ABE≌Rt△CBF，

∴∠EAB=∠FCB，

∴∠FCB=15°，

∴∠ACF=∠FCB+∠BCA=15°+45°=60°，

即∠ACF=60°．