【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.( ![]() =1.732,结果精确到0.1米)
=1.732,结果精确到0.1米)
DEB
参考答案:
【答案】解:∵∠EDG=60°,∠EBG=30°,
∴∠DEB=30°,
∴DE=DB=12米,
在Rt△EDG中,sin∠EDG= ![]() ,
,
∴EG=EDsin∠EDG=12× ![]() =6
=6 ![]() ,
,
∴EF=EG+GF=6 ![]() +1.5≈11.9,
+1.5≈11.9,
答:楼EF的高度约为11.9米
【解析】根据三角形的外角性质,得出∠EDG=∠EDB+∠EBD,即可求出∠DEB的度数,根据等腰三角形的性质得出DE=DB,在Rt△EDG中求出EG的长,根据EF=EG+GF求解。
【考点精析】通过灵活运用解直角三角形和关于仰角俯角问题,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.
-
科目: 来源: 题型:
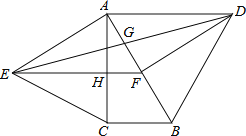
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
 BD
BD其中正确结论的为______(请将所有正确的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形A1B1C1是由三角形ABC经过平移得到的,其中A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如表所示:
三角形ABC
A(0,0)
B(﹣1,2)
C(2,5)
三角形A1B1C1
A1(a,2)
B1(4,b)
C1(7,7)
(1)观察表中各对应点坐标的变化,填空a= ,b= ;
(2)在图中的平面直角坐标系中画出三角形ABC及三角形A1B1C1;
(3)P(m,n)为三角形ABC中任意一点,则平移后对应点P'的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知△ABC,

(1)分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2;
(2)写出△A1B1C1和△A2B2C2各顶点坐标;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的
 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并填空完善下列证明过程:
如图,已知BC⊥AC于C,DF⊥AC于D,∠1+∠2=180°,
求证:∠GFB=∠DEF﹒
证明:∵BC⊥AC于C,DF⊥AC于D(已知),
∴∠C=∠ =90°( ),
∴CB∥FD(同位角相等,两直线平行),
∴∠1+∠3=180°( )
又∵∠1+∠2=180°(已知),
∴∠2=∠3( ),
∴ ∥ ( ),
∴∠GFB=∠DEF( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明同学化简代数式a+2+
 的过程,请仔细阅读并解答所提出的问题. a+2+
的过程,请仔细阅读并解答所提出的问题. a+2+  =2+a+
=2+a+  …第一步
…第一步
=(2+a)(2﹣a)+a2…第二步
=2﹣a2+a2…第三步
=2…第四步
(1)小明的解法从第步开始出现错误,正确的化简结果是;
(2)原代数式的值能等于2吗?为什么?
相关试题

