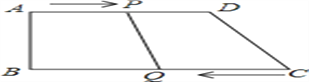
【题目】如图,在四边形ABCD中,AD∥BC, ∠B﹦90°,AB﹦8㎝,AD﹦24㎝,BC﹦26㎝,点p从点A出发,以1㎝/s的速度向点D运动;点Q从点C同时出发,以3㎝/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动. 设运动时间为t s.
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等)
参考答案:
【答案】(1)当t=6时,四边形PQCD是平行四边形.(2)经过7s四边形PQCD是等腰梯形.
【解析】试题分析: (1)根据题意可得PA=t,CQ=3t,则PD=AD-PA=24-t,当PD=CQ时,四边形PQCD为平行四边形,可得方程24-t=3t,解此方程即可求得答案;
(2)过点D作DE⊥BC,则CE=BC-AD=2cm当CQ-PD=4时,四边形PQCD是等腰梯形.即3t-(24-t)=4,求出t的值即可.
试题解析:
(1)运动时间为t s.
AP= t ,PD=24-t,CQ=3t,
经过ts四边形PQCD平行四边形
此时:PD=CQ
∴24-t=3t
解得t=6.
当t=6时,四边形PQCD是平行四边形.
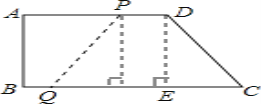
(2)如图,过点D作DE⊥BC,
则CE=BC-AD=2cm.
当CQ-PD=4时,四边形PQCD是等腰梯形.
即3t-(24-t)=4
∴t=7.
∴经过7s四边形PQCD是等腰梯形.
点睛: 此题主要考查了平行四边形、等腰梯形的判定与性质应用,要求学生掌握对各种图形的认识,同时学会数形结合的数学解题思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市城市居民用电收费方式有以下两种:
(甲)普通电价:全天0.53元/度;
(乙)峰谷电价:峰时(早8:00~晚21:00)0.56元/度;谷时(晚21:00~早8:00)0.36元/度.
估计小明家下月总用电量为200度,
⑴若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
⑵请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
⑶到下月付费时, 小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
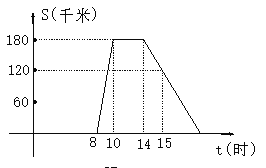
(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求出返程途中S(千米)与时间t (时)的函数关系式,并求出自变量t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校2000名学生的身高情况,随机抽取了该校200名学生测量身高.在这个问题中,样本容量是( )
A. 2000名学生 B. 2000 C. 200名学生 D. 200
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 对顶角相等 B. 内错角相等
C. 相等的角是对顶角 D. 相等的角是内错角
-
科目: 来源: 题型:
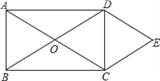
查看答案和解析>>【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2=a,那么x叫做a的平方根.由此可知,4的平方根是_____.
相关试题

