【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

参考答案:
【答案】(1)见解析;(2)OE=2.
【解析】
(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DAC,得出CD=AD=AB,即可得出结论;
(2)先判断出OE=OA=OC,再求出OB=1,利用勾股定理求出OA,即可得出结论.
解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=![]() BD=1,
BD=1,
在Rt△AOB中,AB=![]() ,OB=1,
,OB=1,
∴OA=![]() =2,
=2,
∴OE=OA=2.
-
科目: 来源: 题型:
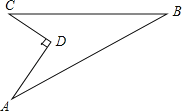
查看答案和解析>>【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场同时出售同样的水瓶和水杯,且定价相同,请根据图中提供的信息,回答下列问题:
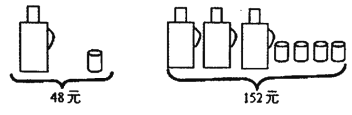
(1)一个水瓶与一个水杯分别是多少元?(请列方程解应用题)
(2)为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和12个水杯,请问选择哪家商场购买更合算,并说明理由(水瓶和水杯必须在同一家购买).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣
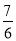 ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;(3)如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】方法感悟:
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
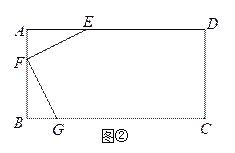
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=
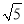 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.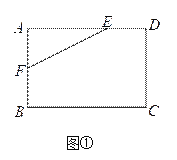
-
科目: 来源: 题型:
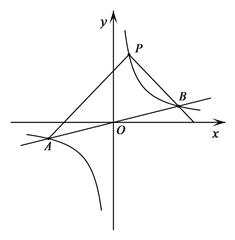
查看答案和解析>>【题目】如图,反比例函数y=
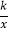 的图象与一次函数y=
的图象与一次函数y=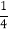 x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=
 ∠AGE.
∠AGE.
相关试题

