Question

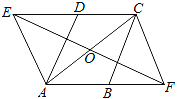
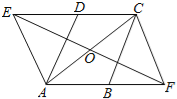
【题目】如图，在ABCD中，∠DAB=60°，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．

（1）求证：四边形AFCE是平行四边形；

（2）若去掉已知条件的“∠DAB=60°”，上述的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．

Answer 1

【答案】（1）见解析；（2）成立，见解析

【解析】试题分析：（1）由已知条件可得△AED，△CFB是正三角形，可得∠AEC=∠BFC=60°，∠EAF=∠FCE=120°，所以四边形AFCE是平行四边形．

（2）上述结论还成立，可以证明△ADE≌△CBF，可得∠AEC=∠BFC，∠EAF=∠FCE，所以四边形AFCE是平行四边形．

（1）证明：∵四边形ABCD是平行四边形，

∴DC∥AB，∠DCB=∠DAB=60°．

∴∠ADE=∠CBF=60°．

∵AE=AD，CF=CB，

∴△AED，△CFB是正三角形．

∴∠AEC=∠BFC=60°，∠EAF=∠FCE=120°．

∴四边形AFCE是平行四边形．

（2）解：上述结论还成立．

证明：∵四边形ABCD是平行四边形，

∴DC∥AB，∠CDA=∠CBA，∠DCB=∠DAB，AD=BC，DC=AB．

∴∠ADE=∠CBF．

∵AE=AD，CF=CB，

∴∠AED=∠ADE，∠CFB=∠CBF．

∴∠AED=∠CFB．

又∵AD=BC，

在△ADE和△CBF中．

，

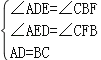∴△ADE≌△CBF（AAS）．

∴∠AED=∠BFC，∠EAD=∠FCB．

又∵∠DAB=∠BCD，

∴∠EAF=∠FCE．

∴四边形EAFC是平行四边形．