【题目】如图,抛物线与![]() 轴交于A(
轴交于A(![]() ,0)、B(
,0)、B(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() 是方程
是方程![]() 的两个根。
的两个根。
(1)求抛物线的解析式;
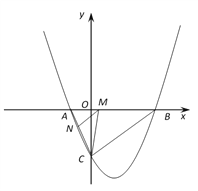
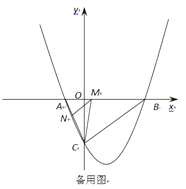
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连接CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点F的坐标,若不存在,请说明理由。
参考答案:
【答案】(1)![]() ;(2)(2,0);(3)
;(2)(2,0);(3)![]() .
.
【解析】试题分析:(1)根据一元二次方程解法得出A,B两点的坐标,再利用交点式求出二次函数解析式;
(2)首先判定△MNA∽△BCA.得出![]() =
=![]() ,进而得出函数的最值;
,进而得出函数的最值;
(3)分别根据当AF为平行四边形的边时,AF平行且等于DE与当AF为平行四边形的对角线时,分析得出符合要求的答案.
试题解析:
(1)∵![]() ,
,
∴![]() ,
, ![]()
∴![]() ,
, ![]()
又∵抛物线过点A、B、C,
故设抛物线的解析式为![]() ,
,
将点C的坐标代入,求得![]()
∴抛物线的解析式为![]()
(2)设点M的坐标为(m,0),过点N作NH⊥x轴于点H
∵点A的坐标为(-2,0),点B的坐标为(6,0),
∴AB=8,AM=m+2。
∵MN∥BC,
∴. △MNA和△BCA相似,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
![]()
![]()
∴当m=2时, ![]() 有最大值4。
有最大值4。
此时,点M的坐标为(2,0)。
(3)∵点D(4,k)在抛物线![]() 上,
上,
∴当x=4时,k=-4,
∴点D的坐标是(4,-4)。
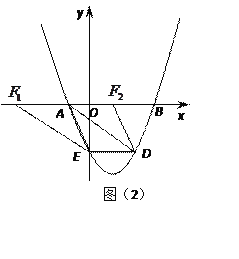
如图(2),当AF为平行四边形的边时,AF![]() DE,AF=DE,
DE,AF=DE,
∵D(4,-4),∴E(0,-4),DE=4。
∴F(-6,0),F(2,0)。
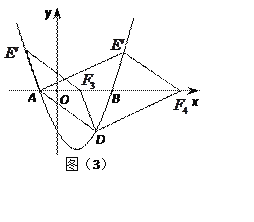
如图(3),当AF为平行四边形的对角线时,
设F(n,0),则平行四边形的对称中心为(![]() ,0)。
,0)。
∴E′的坐标为(n-6,4)。
把E′(n-6,4)代入![]() ,得
,得
![]()
解得 ![]()
∴![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=5cm,回答下列问题:是否存在一点C,使它到A、B两点的距离之和等于4?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红同学要测量A、C两地的距离,但A、C之间有一水池,不能直接测量,于是她在A、C同一水平面上选取了一点B,点B可直接到达A、C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A、C两点之间的距离.(参考数据
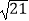 ≈4.6)
≈4.6) 
-
科目: 来源: 题型:
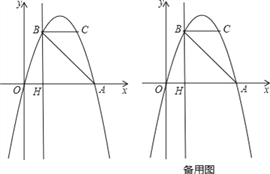
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长分别为10,24,26,则最长边上的中线长为( )
A. 14 B. 13 C. 12 D. 11
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥底面圆的半径为4,母线长为5,它的侧面积等于(结果保留π)
相关试题

