Question

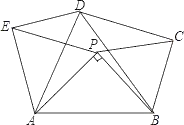
【题目】如图，△APB中，AB=2，∠APB=90°，在AB的同侧作正△ABD、正△APE和正△BPC，则四边形PCDE面积的最大值是__．

Answer 1

【答案】1．

【解析】试题分析：先延长EP交BC于点F，得出PF⊥BC，再判定四边形CDEP为平行四边形，根据平行四边形的性质得出：四边形CDEP的面积=EP×CF=a×b=ab，最后根据，判断ab的最大值即可．

试题解析：延长EP交BC于点F，∵∠APB=90°，∠AOE=∠BPC=60°，∴∠EPC=150°，∴∠CPF=180°﹣150°=30°，∴PF平分∠BPC，又∵PB=PC，∴PF⊥BC，设Rt△ABP中，AP=a，BP=b，则

CF=CP=b， ，∵△APE和△ABD都是等边三角形，∴AE=AP，AD=AB，∠EAP=∠DAB=60°，∴∠EAD=∠PAB，∴△EAD≌△PAB（SAS），∴ED=PB=CP，同理可得：△APB≌△DCB（SAS），∴EP=AP=CP，∴四边形CDEP是平行四边形，∴四边形CDEP的面积=EP×CF=a×b=ab，又∵≥0，∴2ab≤，∴ab≤1，即四边形PCDE面积的最大值为1．故答案为：1．