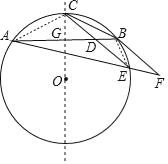
【题目】如图所示AB为⊙O的一条弦，点C为劣弧AB的中点，E为优弧AB上一点，点F在AE的延长线上，且BE=EF，线段CE交弦AB于点D．

（1）求证：CE∥BF；

（2）若BD=2，且EA：EB：EC=3：1：，求△BCD的面积（注：根据圆的对称性可知OC⊥AB）．

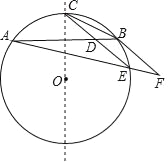
【答案】（1）证明见解析；（2）2.

【解析】分析：（1）连接AC，BE，由等腰三角形的性质和三角形的外角性质得出∠F=∠AEB，由圆周角定理得出∠AEC=∠BEC，证出∠AEC=∠F，即可得出结论；
（2）证明△ADE∽△CBE，得出，证明△CBE∽△CDB，得出，求出CB=，得出AD=6，AB=8，由垂径定理得出OC⊥AB，AG=BG=AB=4，由勾股定理求出CG= =2，即可得出△BCD的面积．

详解：（1）证明：连接AC，BE，作直线OC交AB于G，如图所示：

∵BE=EF，

∴∠F=∠EBF；

∵∠AEB=∠EBF+∠F，

∴∠F=∠AEB，

∵C是的中点，∴，

∴∠AEC=∠BEC，

∵∠AEB=∠AEC+∠BEC，

∴∠AEC=∠AEB，

∴∠AEC=∠F，

∴CE∥BF；

（2）解：∵∠DAE=∠DCB，∠AED=∠CEB，

∴△ADE∽△CBE，

∴，即，

∵∠CBD=∠CEB，∠BCD=∠ECB，

∴△CBE∽△CDB，

∴，即，

∴CB=，

∴AD=6，

∴AB=8，

∵点C为劣弧AB的中点，

∴OC⊥AB，AG=BG=AB=4，

∴CG==2，

∴△BCD的面积=BDCG=×2×2=2．

关闭