【题目】如图,M为正方形ABCD边AB的中点,E是AB延长线上的一点,MN⊥DM,且交∠CBE的平分线于N.
(1)求证:MD=MN;
(2)若将上述条件中的“M为AB边的中点”改为“M为AB边上任意一点”,其余条件不变,则结论“MD=MN”成立吗?如果成立,请证明;如果不成立,说明理由.

参考答案:
【答案】(1)详见解析;(2)成立,理由详见解析.
【解析】
(1)要证MD=MN,就要构建△DFM≌△MBN,只需取AD的中点F,连接FM,依据正方形的性质可证
(2)只需作AF=AM,其余证法与1同.
解:(1)证明:取AD的中点F,连接MF.
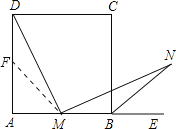
∵四边形ABCD是正方形,M是AB的中点,
∴∠A=∠ABC=90°,DF=AF=AM=MB,
∴∠AFM=45°.
又∵BN平分∠CBE,
∴∠EBN=45°,
∴∠EBN=∠AFM,
∴∠DFM=∠MBN.
又∵∠FDM+∠DMA=90°,
∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∴△FDM≌△BMN,∴MD=NM.
(2)结论“MD=NM”仍然成立.
理由:与(1)类似,在AD上截取DF=MB,连接M.
易得∠FDM=∠BMN,∠DFM=∠MBN,
从而△FDM≌△BMN,∴MD=NM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+
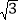 )
)B. 75°和(2,
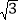 ﹣1)
﹣1)C. 15°和(2,1+
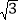 )或75°和(2,
)或75°和(2,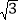 ﹣1)
﹣1)D. 15°和(2,1+
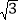 )或75°和(2,1﹣
)或75°和(2,1﹣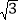 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3b|+(a+b-4)=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
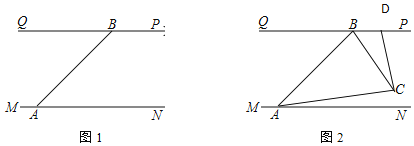
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一只电子狗从原点O出发,按向上→向右→向下→向下→向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示,则A3020的坐标为( )

A.(1007,1)B.(1007,﹣1)C.(504,1)D.(504,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

相关试题

