Question

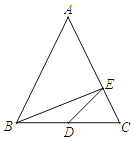
【题目】如图，在△ABC中，AB＝AC，BC＝6，E为AC边上的点且AE＝2EC，点D在BC边上且满足BD＝DE，设BD＝y，S△ABC＝x，则y与x的函数关系式为(　　)

A.y＝x2+B.y＝x2+

C.y＝x2+2D.y＝x2+2

Answer 1

【答案】A

【解析】

过A点作△ABC的高AH，过E点作EG垂直于BC，垂足为G. Rt△EDG中根据勾股定理可用x来表示EG=，由已知可知AH=3EG，即可得到△ABC的面积S△ABC=x

=，通过变形即可得到答案.

解：过A点作△ABC的高AH，过E点作EG垂直于BC，垂足为G.

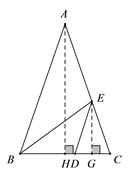
∴EG∥AH，

∴,

又∵AE=2EC，

∴GC=CH，EG=AH

∵AB=AC，BC=6，

∴CH=BH=3，GC=1，BG=5，

在Rt△EDG中，,

∵设BD=y，则DG=5-y，BD=DE=y，

∴EG= =，

∴AH=

∴△ABC的面积S△ABC===，

即：，

∴y＝x2+ 25

故选A