搜索
【题目】写出下列各小题中y关于x的函数表达式，并判断y是否为x的一次函数？是否为x的正比例函数？
(1)长方形的面积为20，长方形的长y与宽x之间的函数表达式．
(2)某地西瓜刚上市时的价格为3.6元/千克，买西瓜的总价y(元)与所买西瓜x(kg)之间的函数表达式．
(3)地面气温为28 ℃，高度每升高1 km，气温下降5 ℃，气温y(℃)与高度x(km)之间的函数表达式．
(4)小林的爸爸为小林存了一份教育储蓄，首次存入10000元，以后每个月存入500元，存入总钱数y(元)与月数x之间的函数表达式．
参考答案：
【答案】(1)y＝
，不是一次函数，也不是正比例函数．
(2)y＝3.6x，是一次函数，也是正比例函数．
(3)y＝28－5x，是一次函数，但不是正比例函数．
(4)y＝10000＋500x，是一次函数，但不是正比例函数．
【解析】（1）y＝
，不是一次函数，也不是正比例函数．
（2）y＝3.6x，是一次函数，也是正比例函数．
（3）y＝28－5x，是一次函数，但不是正比例函数．
（4）y＝500x+10000，是一次函数，但不是正比例函数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】地球绕太阳公转的速度约为110000km/h，则110000用科学记数法可表示为（ ）
A.0.11×106
B.1.1×105
C.0.11×105
D.1.1×106 -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小明遇到这样一个问题：
如图1，△ABC中，∠A=90°，∠B=30°，点D，E分别在AB，BC上，且∠CDE=90°．当BE=2AD时，图1中是否存在与CD相等的线段？若存在，请找出并加以证明，若不存在，说明理由．
小明通过探究发现，过点E作AB的垂线EF，垂足为F，能得到一对全等三角形（如图2），从而将解决问题．
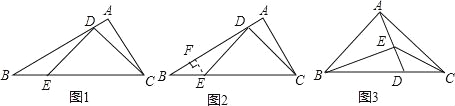
请回答：
（1）小明发现的与CD相等的线段是 ．
（2）证明小明发现的结论；
参考小明思考问题的方法，解决下面的问题：
（3）如图3，△ABC中，AB=AC，∠BAC=90°，点D在BC上，BD=2DC，点E在AD上，且∠BEC=135°，求
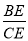的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，两个全等的△ABC和△DEF中，∠ACB=∠DFE=90°，AB=DE，其中点B和点D重合，点F在BC上，将△DEF沿射线BC平移，设平移的距离为x，平移后的图形与△ABC重合部分的面积为y，y关于x的函数图象如图2所示（其中0≤x≤m，m＜x≤3，3＜x≤4时，函数的解析式不同）
（1）填空：BC的长为 ；
（2）求y关于x的函数关系式，并写出x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知多项式A=x2+2y2﹣z2 ， B=﹣4x2+3y2+2z2且A+B+C=0，则C为（ ）
A.5x2﹣y2﹣z2
B.3x2﹣5y2﹣z2
C.3x2﹣y2﹣3z2
D.3x2﹣5y2+z2 -
科目： 来源： 题型：
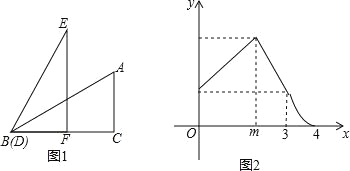
查看答案和解析>>【题目】某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物，装卸货物共用45 min，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60 km/h，两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示，有下列结论：①快递车从甲地到乙地的速度为100 km/h；②甲、乙两地之间的距离为120 km；③图中点B的坐标为(3.75，75)；④快递车从乙地返回时的速度为90 km/h.其中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①③
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一次函数y=2x＋m的图像与x轴相交于点A（－3，0），则m的值为（ ）
A.－3B.6C.－6D.6或－6
相关试题
