【题目】一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.
A. 35B. 40C. 45D. 50
参考答案:
【答案】C
【解析】
设第一次他看到的两位数的个位数为x,十位数为y,汽车行驶速度为v,第一次看到的两位数为10y+x,行驶一小时后看到的两位数为10x+y,第三次看到的三位数为100y+x,由汽车均速行驶可得三段时间的路程相等,即可列出两个方程求解即可.由速度=![]() ,求得答案.
,求得答案.
设第一次他看到的两位数的个位数为![]() ,十位数为
,十位数为![]() ,汽车行驶速度为
,汽车行驶速度为![]() ,根据题意得:
,根据题意得:
 ,
,
解得:![]() ,
,
∵![]() 为1-9内的自然数,
为1-9内的自然数,
∴![]() ;
;
即两位数为16.
即:第一次看到的两位数是16.
第二次看到的两位数是61.
第三次看到的两位数是106.
则汽车的速度是:![]() (千米/小时).
(千米/小时).
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c与直线y=
 x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
-
科目: 来源: 题型:
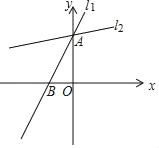
查看答案和解析>>【题目】如图,已知直线l1:y=2x+4与y轴交于A点,与x轴交于点B,经过A点的直线l2与直线l1所夹的锐角为45°.
(1)过点B作CB⊥AB,交l2于C,求点C的坐标.
(2)求l2的函数解析式.
(3)在直线l1上存在点M,直线l2上存在点N,使得点A、O、M、N四点组成的四边形是平行四边形,请直接写出点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,路边有一灯杆AB,在A点灯光的照耀下,点D处一直立标杆CD的影子为DH,沿BD方向的F处有另一标杆EF,其影子为FG,
(1)在图中画出灯杆AB,并标上相应的字母;(不写画法,保留画图痕迹)
(2)已知标杆EF=1.6m,影长FG=4m,灯杆AB到标杆EF的距离BF=8m,求灯杆AB的长.
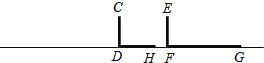
-
科目: 来源: 题型:
查看答案和解析>>【题目】两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(
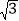 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)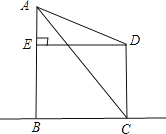
相关试题

