【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积. 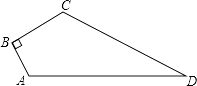
参考答案:
【答案】解:连接AC,如图所示: 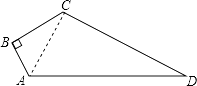
∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC= ![]() =5,
=5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2 ,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD= ![]() ABBC+
ABBC+ ![]() ACCD=
ACCD= ![]() ×3×4+
×3×4+ ![]() ×5×12=36.
×5×12=36.
故四边形ABCD的面积是36.
【解析】连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.
-
科目: 来源: 题型:
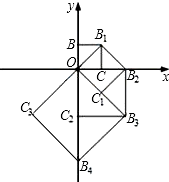
查看答案和解析>>【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1 , 以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 , 再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 , …,依次进行下去,则点B6的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
 (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)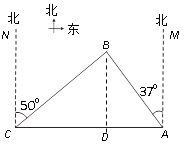
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:33+(-32)+7-(-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对九年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):3.5,4,3.5,5,5,3.5.这组数据的众数是( )
A. 3 B. 3.5 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣3x﹣4=0的一次项系数是( )
A.1B.﹣3C.3D.﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名身高为1.6m的同学的影长为1.2m,同一时刻旗杆影长为9m,那么旗杆的高度是_____m.
相关试题

