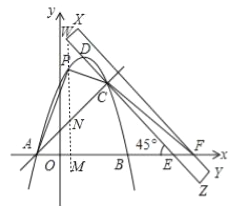
【题目】如图,已知抛物线y=ax2+2x+6(a≠0)交x轴与A,B两点(点A在点B左侧),将直尺WXYZ与x轴负方向成45°放置,边WZ经过抛物线上的点C(4,m),与抛物线的另一交点为点D,直尺被x轴截得的线段EF=2,且△CEF的面积为6.
(1)求该抛物线的解析式;
(2)探究:在直线AC上方的抛物线上是否存在一点P,使得△ACP的面积最大?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由.
(3)将直尺以每秒2个单位的速度沿x轴向左平移,设平移的时间为t秒,平移后的直尺为W′X′Y′Z′,其中边X′Y′所在的直线与x轴交于点M,与抛物线的其中一个交点为点N,请直接写出当t为何值时,可使得以C、D、M、N为顶点的四边形是平行四边形.

参考答案:
【答案】(1)=﹣![]() x2+2x+6;(2)在直线AC上方的抛物线上存在一点P,使得△ACP的面积最大,面积的最大值为
x2+2x+6;(2)在直线AC上方的抛物线上存在一点P,使得△ACP的面积最大,面积的最大值为![]() ,此时点P的坐标为(1,
,此时点P的坐标为(1,![]() );(3)当t为4﹣
);(3)当t为4﹣![]() 或4+
或4+![]() 秒时,可使得以C、D、M、N为顶点的四边形是平行四边形.
秒时,可使得以C、D、M、N为顶点的四边形是平行四边形.
【解析】
试题分析:(1)根据三角形的面积公式求出m的值,结合点C的坐标利用待定系数法即可求出a值,从而得出结论;(2)假设存在.过点P作y轴的平行线,交x轴与点M,交直线AC于点N.根据抛物线的解析式找出点A的坐标.设直线AC的解析式为y=kx+b,点P的坐标为(n,﹣![]() n2+2n+6)(﹣2<n<4),由点A、C的坐标利用待定系数法即可求出直线AC的解析式,代入x=n,即可得出点N的坐标,利用三角形的面积公式即可得出S△ACP关于n的一元二次函数,根据二次函数的性质即可解决最值问题;(3)根据直尺的摆放方式可设出直线CD的解析式为y=﹣x+c,由点C的坐标利用待定系数法即可得出直线CD的解析式,联立直线CD的解析式与抛物线的解析式成方程组,解方程组即可求出点D的坐标,令直线CD的解析式中y=0,求出x值即可得出点E的坐标,结合线段EF的长度即可找出点F的坐标,设出点M的坐标,结合平行四边形的性质以及C、D点坐标的坐标即可找出点N的坐标,再由点N在抛物线图象上,将其代入抛物线解析式即可得出关于时间t的一元二次方程,解方程即可得出结论.
n2+2n+6)(﹣2<n<4),由点A、C的坐标利用待定系数法即可求出直线AC的解析式,代入x=n,即可得出点N的坐标,利用三角形的面积公式即可得出S△ACP关于n的一元二次函数,根据二次函数的性质即可解决最值问题;(3)根据直尺的摆放方式可设出直线CD的解析式为y=﹣x+c,由点C的坐标利用待定系数法即可得出直线CD的解析式,联立直线CD的解析式与抛物线的解析式成方程组,解方程组即可求出点D的坐标,令直线CD的解析式中y=0,求出x值即可得出点E的坐标,结合线段EF的长度即可找出点F的坐标,设出点M的坐标,结合平行四边形的性质以及C、D点坐标的坐标即可找出点N的坐标,再由点N在抛物线图象上,将其代入抛物线解析式即可得出关于时间t的一元二次方程,解方程即可得出结论.
试题解析:解:(1)∵S△CEF=![]() EFyC=
EFyC=![]() ×2m=6,
×2m=6,
∴m=6,即点C的坐标为(4,6),
将点C(4,6)代入抛物线y=ax2+2x+6(a≠0)中,
得:6=16a+8+6,解得:a=﹣![]() ,
,
∴该抛物线的解析式为y=﹣![]() x2+2x+6.
x2+2x+6.
(2)假设存在.过点P作y轴的平行线,交x轴与点M,交直线AC于点N,如图1所示.
令抛物线y=﹣![]() x2+2x+6中y=0,则有﹣
x2+2x+6中y=0,则有﹣![]() x2+2x+6=0,
x2+2x+6=0,
解得:x1=﹣2,x2=6,
∴点A的坐标为(﹣2,0),点B的坐标为(6,0).
设直线AC的解析式为y=kx+b,点P的坐标为(n,﹣![]() n2+2n+6)(﹣2<n<4),
n2+2n+6)(﹣2<n<4),
∵直线AC过点A(﹣2,0)、C(4,6),
∴![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为y=x+2.
∵点P的坐标为(n,﹣![]() n2+2n+6),
n2+2n+6),
∴点N的坐标为(n,n+2).
∵S△ACP=![]() PN(xC﹣xA)=
PN(xC﹣xA)=![]() ×(﹣
×(﹣![]() n2+2n+6﹣n﹣2)×[4﹣(﹣2)]=﹣
n2+2n+6﹣n﹣2)×[4﹣(﹣2)]=﹣![]() (n﹣1)2+
(n﹣1)2+![]() ,
,
∴当n=1时,S△ACP取最大值,最大值为![]() ,
,
此时点P的坐标为(1,![]() ).
).
∴在直线AC上方的抛物线上存在一点P,使得△ACP的面积最大,面积的最大值为![]() ,此时点P的坐标为(1,
,此时点P的坐标为(1,![]() ).
).
(3)∵直尺WXYZ与x轴负方向成45°放置,
∴设直线CD的解析式为y=﹣x+c,
∵点C(4,6)在直线CD上,
∴6=﹣4+c,解得:c=10,
∴直线CD的解析式为y=﹣x+10.
联立直线CD与抛物线解析式成方程组: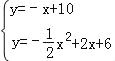 ,
,
解得:![]() ,或
,或![]() ,
,
∴点D的坐标为(2,8).
令直线CD的解析式y=﹣x+10中y=0,则0=﹣x+10,
解得:x=10,即点E的坐标为(10,0),
∵EF=2,且点E在点F的左边,
∴点F的坐标为(12,0).
设点M的坐标为(12﹣2t,0),则点N的坐标为(12﹣2t﹣2,0+2),即N(10﹣2t,2).
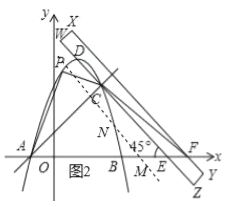
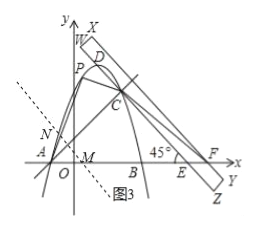
∵点N(10﹣2t,2)在抛物线y=﹣![]() x2+2x+6的图象上,
x2+2x+6的图象上,
∴﹣![]() (10﹣2t)2+2(10﹣2t)+6=2,整理得:t2﹣8t+13=0,
(10﹣2t)2+2(10﹣2t)+6=2,整理得:t2﹣8t+13=0,
解得:t1=4﹣![]() ,t2=4+
,t2=4+![]() .
.
∴当t为4﹣![]() 或4+
或4+![]() 秒时,可使得以C、D、M、N为顶点的四边形是平行四边形.
秒时,可使得以C、D、M、N为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知4y2+my+9是完全平方式,则m为( )
A.6
B.±6
C.±12
D.12 -
科目: 来源: 题型:
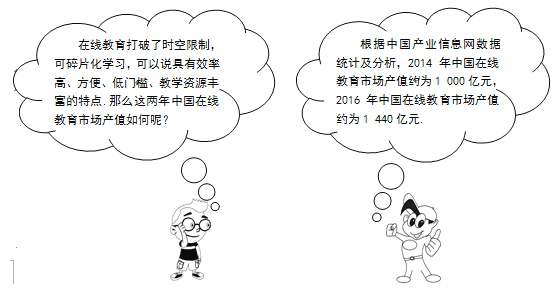
查看答案和解析>>【题目】“在线教育”指的是通过应用信息科技和互联网技术进行内容传播和快速学习的方法.“互联网+”时代,中国的在线教育得到迅猛发展. 请根据下面张老师与记者的对话内容,求2014年到2016年中国在线教育市场产值的年平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学的部分学生参加该市中学生知识竞赛,小王同学统计了所有参赛同学的成绩,并且根据学过的知识绘制了统计图.请根据图中提供的信息回答问题:
(1)该校参加本竞赛的同学共_________人;
(2)若成绩在6分以上的(含6分)的同学获奖,则该校参赛同学的获奖率为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示:0.0018= .
-
科目: 来源: 题型:
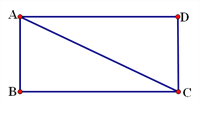
查看答案和解析>>【题目】如图,有一个长方形花园,对角线AC是一条小路,现要在AD边上找一个位置建报亭,使报亭到小路两端点A、C的距离相等.
(1)用尺规作图的方法,在图中找出报亭位置(不写作法,但需保留作图痕迹,交代作图结果);
(2)如果AD=80m,CD=40m,求报亭到小路端点A的距离.
相关试题

