【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

参考答案:
【答案】2.5
【解析】试题分析:∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,∴DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°,∵∠EDF=45°,∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,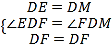 ,∴△DEF≌△DMF(SAS),∴EF=MF,设EF=MF=x,
,∴△DEF≌△DMF(SAS),∴EF=MF,设EF=MF=x,
∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM﹣MF=BM﹣EF=4﹣x,
∵EB=AB﹣AE=3﹣1=2,在Rt△EBF中,由勾股定理得EB2+BF2=EF2, 即22+(4﹣x)2=x2,
解得:x=![]() , ∴FM=
, ∴FM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=x与双曲线y=
 相交于点A(a,2),将直线l1向上平移3个单位得到l2 , 直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
相交于点A(a,2),将直线l1向上平移3个单位得到l2 , 直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点. 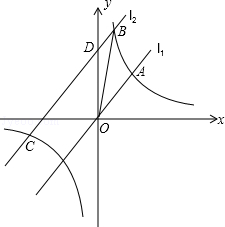
(1)求双曲线y= 的解析式;
的解析式;
(2)求tan∠DOB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州国际动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,动漫公司又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司两次共购进这种玩具多少套?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M为直线AB上一动点,
 都是等边三角形,连接BN
都是等边三角形,连接BN  求证:
求证:  ;
; 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系 不需证明
不需证明 ;
; 如图4,当
如图4,当 时,证明:
时,证明:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

-
科目: 来源: 题型:
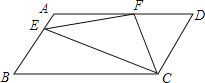
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,
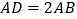 ,F是AD的中点,作
,F是AD的中点,作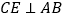 ,垂足E在线段上,连接EF、CF,则下列结论
,垂足E在线段上,连接EF、CF,则下列结论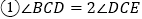 ;
;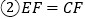 ;
;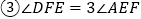 ,
,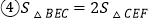 中一定成立的是______
中一定成立的是______  把所有正确结论的序号都填在横线上
把所有正确结论的序号都填在横线上
相关试题

