【题目】已知:在四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF相交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证:![]() ;
;
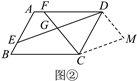
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=9,DA=DC=12,∠BAD=90°,DE⊥CF.求![]() 的值.
的值.

参考答案:
【答案】(1)详见解析;(2))当∠B=∠EGC或∠B+∠EGC=180°时,![]() 成立,证明详见解析;(3)
成立,证明详见解析;(3)![]() .
.
【解析】
(1)由矩形的性质得出∠A=∠ADC=90°,由角的互余关系整除∠ADE=∠DCF,即可得出△ADE∽△DCF;
(2)在AD的延长线上取点M,使CM=CF,由等腰三角形的性质得出∠CMF=∠CFM.由平行四边形的性质得出∠A=∠CDM,∠FCB=∠CFM,证出∠BEG+∠FCB=180°,得出∠AED=∠FCB,因此∠CMF=∠AED.证明△ADE∽△DCM,得出对应边成比例得![]() 即可得出结论;
即可得出结论;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,建立方程求出求出CN,最后用相似三角形的性质即可得出结论.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠ADE+∠CDG=90°.
∵DE⊥CF,
∴∠CDG+∠DCF=90°,
∴∠ADE=∠DCF.
又∵∠A=∠CGD=90°,
∴△ADE∽△GCD,
∴![]() 即
即![]()
(2)当∠B=∠EGC或∠B+∠EGC=180°时,![]() 成立.
成立.
证明:当∠B=∠EGC时,过点C作DE的平行线,过点D作CF的平行线,两线交于点M,如图①,∴四边形CMDG是平行四边形,
∴CG=DM,∠M=∠CGD,∠CDG=∠DCM.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A+∠B=180°,∠FCB=∠CFD.
∵∠B=∠EGC,∴∠A+∠EGC=180°.
∵∠EGC+∠CGD=180°,
∴∠A=∠CGD,
∴∠A=∠CGD=∠M.
∵AB∥CD,
∴∠AED=∠CDG.
∵∠CDG=∠DCM,
∴∠AED=∠DCM,
∴△ADE∽△MDC,
∴![]()
∵CG=DM,
∴![]()
即![]()
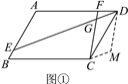
当∠B+∠EGC=180°时,过点C作DE的平行线,过点D作CF的平行线,两线交于点M,如图②,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠CFD=∠BCF.
∵∠B+∠EGC=180°,
∴∠GEB+∠BCF=180°,
∴∠BCF=∠AED,
∴∠CFD=∠AED.
∵∠ADE=∠GDF,
∴△FDG∽△EDA,
∴![]() ,即
,即![]()
∵AB∥CD,∴∠AED=∠CDE,
∴∠CFD=∠CDE.
∵∠FCD=∠DCG,
∴△FCD∽△DCG,
∴![]()
∴![]()
∴![]()
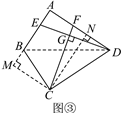
(3)如图③,过点C作CN⊥AD于点N,CM⊥AB交AB的延长线于点M,连接BD,设CN=x,
∵∠BAD=90°,
∴∠A=∠M=∠CAN=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM.
∵在△BAD和△BCD中,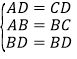
∴△BAD≌△BCD,
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°.
∵∠ABC+∠MBC=180°,
∴∠MBC=∠ADC.
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() 即
即![]() ,∴
,∴![]()
在Rt△CMB中,![]() ,BM=AM-AB=x-9,
,BM=AM-AB=x-9,
由勾股定理,得BM2+CM2=BC2,
∴![]()
解得x1=0(舍去),![]()
∴![]()
∵∠A=∠FGE=90°,
∴∠AED+∠AFG=180°.
∵∠AFG+∠NFC=180°,
∴∠/span>AED=∠NFC.
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.

(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为______和位置关系为______;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?写出结论,证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016辽宁省葫芦岛市)甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形A1B1C1O、A2B2C2C1……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4),则B2019的坐标是_____.

-
科目: 来源: 题型:
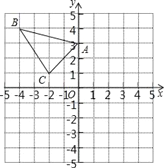
查看答案和解析>>【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
相关试题

