【题目】学校开展综合实践活动中,某班进行了小制作评比,作品上交时间为5月11日至5月30日,评委们把同学们上交作品的件数按5天一组分组统计,绘制了频数分 布直方图如下,小长方形的高之比为:2:5:2:1.现已知第二组的上交作品件数是20件.求: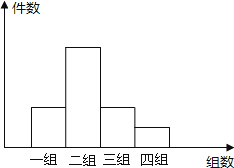
(1)此班这次上交作品共多少件?
(2)评委们一致认为第四组的作品质量都比较高,现从中随机抽取2件作品参加学校评比,小明的两件作品都在第四组中,他的两件作品都被抽中的概率是多少?(请写出解答过程)
参考答案:
【答案】
(1)
![]()
答:此班这次上交作品共40件。
(2)
设四件作品编号为1、2、3、4号,小明的两件作品分别为1、2号.
列举:(1,2);(1,3);(1,4); (2,3);(2,4);(3,4).
所以他的两件作品都被抽中的概率是 ![]() .
.
【解析】本题考查了条形统计图及列表法和树状图的知识,解题的关键是了解直方图中每一个小长方形的高的比等于它们频数的比.(1)用第二小组的频数除以该小组的份数占总份数的多少即可求得总人数;(2)分别列举出所有可能结果后用概率的公式即可求解.另:构成树状图,或用表格法求解等方法,答案正确相应给分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

-
科目: 来源: 题型:
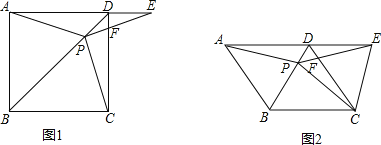
查看答案和解析>>【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD.
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=
 ∠MBE,∠CDN=
∠MBE,∠CDN= ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则 = .
= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有质地均匀的A、B、C、D四张卡片,上面对应的图形分别是圆、正方形、正三角形、平行四边形,将这四张卡片放入不透明的盒子中摇匀,从中随机抽出一张(不放回),再随机抽出第二张.
(1)如果要求抽出的两张卡片上的图形,既有圆又有三角形,请你用列表或画树状图的方法,求出出现这种情况的概率.
(2)因为四张卡片上有两张上的图形,既是中心对称图形,又是轴对称图形,所以小明和小东约定做一个游戏,规则是:如果抽出的两个图形,既是中心对称图形又是轴对称图形,则小明赢;否则,小东赢.问这个游戏公平吗?为什么?如果不公平,请你设计一个公平的游戏规则. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( ).
A.“打开电视机,正在播放《动物世界》”是必然事件
B.某种彩票的中奖概率为 ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C.抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为
D.想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛一枚均匀硬币正面朝上的概率为
 ,下列说法正确的是( ).
,下列说法正确的是( ).
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次,不可能正面都朝上
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
相关试题

