【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.

(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
参考答案:
【答案】(1)∠M=450;(2)当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.
【解析】(1)首先作MQ∥AB,根据平行线的性质,推得![]() 然后根据HP⊥EF,推得
然后根据HP⊥EF,推得![]() 据此求出∠M的度数即可.
据此求出∠M的度数即可.
(2)①首先判断出∠NEQ=∠NEF+∠QEF=![]()
然后根据NQ⊥EM,可得![]() 推得
推得![]() 再根据AB∥CD,推得∠FHE=∠CEH=2∠ENQ.即可.
再根据AB∥CD,推得∠FHE=∠CEH=2∠ENQ.即可.
②首先判断出∠NEQ=∠QEF∠NEF![]()
然后根据NQ⊥EM,可得![]() 推得
推得![]() 再根据AB∥CD,推得
再根据AB∥CD,推得![]() 即可.
即可.
(1)如图1,作MQ∥AB,

∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴![]()
∵HP⊥EF,
∴![]()
∴![]()
∵∠1+∠2=∠M,
∴![]()
(2)①如图2,

∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=![]()
∵NQ⊥EM,
∴![]()
∴![]()
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图

![]() 理由如下:
理由如下:
∠NEQ=∠QEF∠NEF![]()
∵NQ⊥EM,
∴![]()
∴![]()
∵AB∥CD,
∴![]()
综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知am=2,an=3.求am+n的值;
(2)已知n为正整数,且x2n=7.求7(x3n)2﹣3(x2)2n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出函数
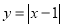 的图象.
的图象. (1)函数
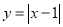 的自变量x的取值范围是________;
的自变量x的取值范围是________;(2)列表(把表格补充完整)
x
……
-2
-1
0
1
2
3
4
……
y
(3)描点、连线
(4)结合图象,写出函数的一条性质________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,
(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;
(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;
(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AB=AC,∠ABC=60°,AD=CE,求∠BPD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

相关试题

