Question

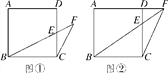
【题目】已知正方形ABCD，点E在边CD上，点F在线段BE的延长线上，连接FC，且∠FCE＝∠CBE.

(1)如图①，当点E为CD边的中点时，求证：CF＝2EF；

(2)如图②，当点F位于线段AD的延长线上时，求证： .

Answer 1

【答案】（1）见解析 （2）见解析

证明：(1)∵四边形ABCD是正方形，

∴CD＝BC.∵点E为CD边的中点，

∴CE＝CD＝BC.

∵∠FCE＝∠CBE，∠F＝∠F，∴△FCE∽△FBC，

∴

又∵CE＝BC，∴＝，∴CF＝2EF.

(2)∵四边形ABCD是正方形，∴DE∥AB，AD∥BC，AD＝CD，∴ ＝，

∴＝.∵AF∥BC，∴∠DFE＝∠CBE.∵∠FCE＝∠CBE，∴∠DFE＝∠FCE.又∵∠FDE＝∠CDF，∴△FDE∽△CDF，∴＝，∴＝.

【解析】试题分析：根据正方形的性质得到，由点为边的中点，得到 根据相似三角形的性质即可得到结论；

根据正方形的性质得到 根据平行线分线段成比例定理得到等量代换得到 根据相似三角形的性质得到

于是得到结论．

试题解析：(1)∵四边形ABCD是正方形，

∴CD＝BC.

∵点E为CD边的中点，

∵∠FCE＝∠CBE，∠F＝∠F，

∴△FCE∽△FBC，

又∵

∴CF＝2EF.

(2)∵四边形ABCD是正方形，

∴DE∥AB，AD∥BC，AD＝CD，

∵AF∥BC，

∴∠DFE＝∠CBE.

∵∠FCE＝∠CBE，

∴∠DFE＝∠FCE.

又∵∠FDE＝∠CDF，

∴△FDE∽△CDF，