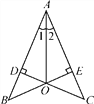
【题目】如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE,CD相交于点O,连接AO.求证:
(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
参考答案:
【答案】见解析
【解析】试题分析:(1)、根据角平分线的性质得出OD=OE,然后证明△BOD和△COE全等,从而得出答案;(2)、根据题意得出△BOD和△COE全等,从而得出OD=OE,然后根据角平分线性质定理的逆定理得出答案.
试题解析:(1)、∵∠1=∠2 ∴AO平分∠BAC,∴OD=OE,
又∵∠BDO=∠CEO=90°,∠BOD=∠COE, ∴△BOD≌△COE(ASA),∴OB=OC;
(2)、 ∵∠BDO=∠CEO=90°,∠BOD=∠COE,OB=OC,
∴△BOD≌△COE(AAS),∴OD=OE,
又∵CD⊥AB,BE⊥AC,垂足分别为D、E, ∴OA平分∠BAC,即∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读某同学对多项式
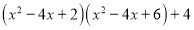 进行因式分解的过程,并解决问题:
进行因式分解的过程,并解决问题:解:设
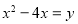 ,
,原式
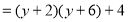 (第一步)
(第一步)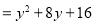 (第二步)
(第二步)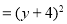 (第三步)
(第三步)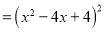 (第四步)
(第四步)(1)该同学第二步到第三步的变形运用了________(填序号);
A.提公因式法 B.平方差公式
C.两数和的平方公式 D.两数差的平方公式
(2)该同学在第三步用所设的的代数式进行了代换,得到第四步的结果,这个结果能否进一步因式分解?________(填“能”或“不能”).如果能,直接写出最后结果________.
(3)请你模仿以上方法尝试对多项式
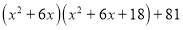 进行因式分行解.
进行因式分行解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,过点O作射线OC,使
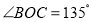 .将一个含
.将一个含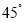 角的直角三角板OMN的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边ON,MN都在直线AB的下方.
角的直角三角板OMN的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边ON,MN都在直线AB的下方.
(1)将图1中的三角板OMN绕着点O逆时针旋转
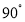 ,如图2所示,请问OM是否平分
,如图2所示,请问OM是否平分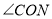 ?请说明理由;
?请说明理由;(2)将图2中的三角板OMN绕点O逆时针继续旋转到图3的位置所示,使得ON在
 的内部,请探究
的内部,请探究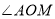 与
与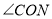 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;(3)将图1中的三角板OMN绕点O按每秒
 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直角边ON所在直线恰好平分锐角
的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直角边ON所在直线恰好平分锐角 ,则t的值为________(直接写出结果).
,则t的值为________(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到学校上学,沿途需经过三个路口,每个路口都设有红、绿两种颜色的信号灯,在信号灯正常情况下:
(1)请用树状图列举小明遇到交通信号灯的所有情况;
(2)小明遇到两次绿色信号的概率有多大?
(3)小明红绿色两种信号都遇到的概率有多大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用抽样调查的是( )
A.对某地区现有的
 名百岁以上老人睡眠时间的调查
名百岁以上老人睡眠时间的调查B.对“神舟十一号”运载火箭发射前零部件质量情况的调查
C.对某校七年级三班学生视力情况的调查
D.对株洲市民与长沙市民是否了解“株洲南雅实验中学高复班”的调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有
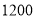 名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了
名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了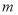 名学生进行抽样调查,整理样本数据,得到下列图表(频数分布表中部分划记被污染渍盖住):
名学生进行抽样调查,整理样本数据,得到下列图表(频数分布表中部分划记被污染渍盖住):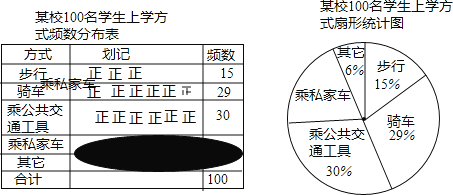
(1)
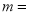 ;
;(2)求扇形统计图中,乘私家车部分对应的圆心角的度数;
(3)请估计该校
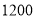 名学生中,选择骑车和步行上学的一共有多少人?
名学生中,选择骑车和步行上学的一共有多少人?
相关试题

