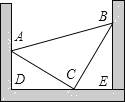
【题目】如图，一个等腰直角三角形零件放置在一凹槽内，顶点A.B.C分别落在凹槽内壁上，测得AD＝5cm，BE＝9cm，则该零件的面积为 _______ 　　　　

【答案】53cm2

【解析】

首先证明△ADC≌△CEB，根据全等三角形的性质可得DC=BE=9cm，再利用勾股定理计算出AC长，然后利用三角形的面积公式计算出该零件的面积即可．

解：∵△ABC是等腰直角三角形，

∴AC=BC，∠ACB=90°，

∴∠ACD+∠BCE=90°，

∵∠ADC=90°，

∴∠ACD+∠DAC=90°，

∴∠DAC=∠BCE，

在△ADC和△CEB中，，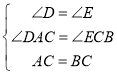

∴△ADC≌△CEB（AAS），

∴DC=BE=9cm，

∴AC===（cm），

∴BC=cm，

∴该零件的面积为：××=53（cm2）．

故答案为：53cm2．

关闭