【题目】如图,已知抛物线![]() (其中
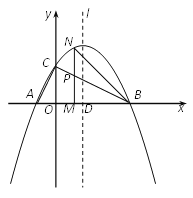
(其中![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
参考答案:
【答案】(1)抛物线的关系式为![]() ;
;
(2)点E的坐标为![]() 或
或![]()
【解析】试题分析:(1)由题意可求得点![]() 、
、![]() 、
、![]()
试题解析:
(1)求得点![]() 、
、![]() 、
、![]()
易得∠ACB=90°,由△AOC∽△COB可得![]()
∴![]()
(2)易证∠ACO=∠CBO,∠MNB=∠MBN,所以∠BED=∠CBN
连结CN, 由勾股定理得CN=![]() ,BC=
,BC=![]() ,BN=
,BN=![]() , 由勾股定理逆定理证得∠CNB=90°,从而得
, 由勾股定理逆定理证得∠CNB=90°,从而得![]()
然后解Rt△BED可得DE=![]() ,
,
∴点E坐标为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=(k﹣1)x+3的图象经过点(﹣2,1),则k的值是( )
A. ﹣1B. 2C. 1D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】现用甲、乙两种运输车将46t抗旱物资运往灾区,甲种运输车载重5t,乙种运输车载重4t,安排车辆不超过10辆,则甲种运输车至少应安排( )
A.4辆
B.5辆
C.6辆
D.7辆 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制如图不完整的条形统计图和扇形统计图.
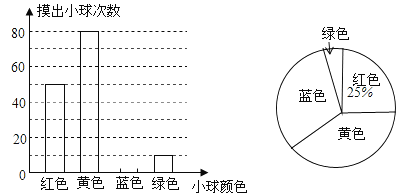
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(0.125)2015×(﹣8)2016的结果等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )

A.15cm
B.13cm
C.11cm
D.9cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=
 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 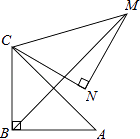
相关试题

