Question

【题目】如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F.

(1)求证：DF⊥AC；

(2)若⊙O的半径为5，∠CDF=30°，求的长(结果保留π)．

Answer 1

【答案】（1）证明见解析；（2）的长为.

【解析】试题分析：（1）连接OD，由切线的性质即可得出∠ODF=90°，再由BD=CD，OA=OB可得出OD是△ABC的中位线，根据三角形中位线的性质即可得出，根据平行线的性质即可得出∠CFD=∠ODF=90°，从而证出DF⊥AC；

（2）由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°，再结合OB=OD可得出△OBD是等边三角形，根据弧长公式即可得出结论．

试题解析：（1）证明：连接OD，如图所示．

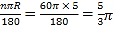
∵DF是⊙O的切线，D为切点，

∴OD⊥DF，

∴∠ODF=90°

∵BD=CD，OA=OB，

∴OD是△ABC的中位线，

∴OD∥AC，

∴∠CFD=∠ODF=90°，

∴DF⊥AC．

（2）解：∵∠CDF=30°，

由（1）得∠ODF=90°，

∴∠ODB=180°-∠CDF-∠ODF=60°

∵OB=OD，

∴△OBD是等边三角形，

∴∠BOD=60°，

∴BD弧的长=