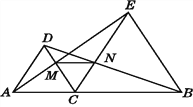
【题目】如图,点C是线段AB上任意一点(点C与点A,B不重合),分别以AC,BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.连接MN.
试说明:(1)△ACM≌△DCN;(2)MN∥AB.
参考答案:
【答案】见解析
【解析】试题分析: ![]() 由已知条件可利用两边及其夹角相等的三角形全等得△ACE≌△DCB. 由全等三角形的性质可得∠CAE=∠CDB,接下来根据两角及其夹边相等的三角形全等即可得到结论;
由已知条件可利用两边及其夹角相等的三角形全等得△ACE≌△DCB. 由全等三角形的性质可得∠CAE=∠CDB,接下来根据两角及其夹边相等的三角形全等即可得到结论;
![]() 证明第一问的方法类似,可证得△BCN≌△ECM,进而可以得出△CMN是等边三角形,
证明第一问的方法类似,可证得△BCN≌△ECM,进而可以得出△CMN是等边三角形,
试题解析:(1)∵ △ACD、△BCE为等边三角形,
![]()
![]()
![]()
∴ △ACE≌△DCB.
∴ ∠CAE=∠CDB,
∵ ∠DCA=∠BCE=60°,
∴ ∠DCE=60°,
∵ ∠CAE=∠CDB,AC=CD,∠ACD=∠DCE,
∴ △ACM≌△DCN.
(2)∵ △ACE≌△BCD,
∴ ∠MEC=∠NBC,
∵ ∠BCE=∠ECM=60°,BC=CE,∠MEC=∠NBC,
∴ △BCN≌△ECM,
∴ CM=CN,
∵ CM=CN,∠ECM=60°,
∴ △CMN是等边三角形,
∴ ∠MNC=60°,
∵ ∠BCE=∠MNC=60°,
∴ MN∥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )

A. 3 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程(a﹣2)x2﹣3x+a-1=0是一元二次方程,则( )
A.a≠2B.a>2C.a=0D.a>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P1(-4,3)和P2(-4,-3),则P1和P2( )
A. 关于原点对称 B. 关于y轴对称
C. 关于x轴对称 D. 不存在对称关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA⊥射线OB,半径
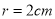 的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM
的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM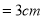 .设OP=
.设OP= 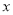
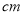 ,OQ=
,OQ= 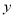
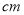 .
.(1)求
 、
、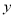 所满足的关系式,并写出
所满足的关系式,并写出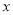 的取值范围 ;
的取值范围 ;(2)当△MOP为等腰三角形时,求相应
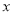 的值;
的值; (3)是否存在大于2的实数
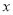 ,使△MQO∽△OMP?若存在,求相应
,使△MQO∽△OMP?若存在,求相应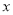 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.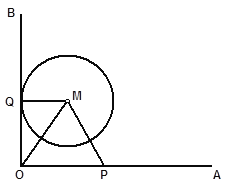
-
科目: 来源: 题型:
查看答案和解析>>【题目】气象部门检测到某一天上午的温度是5℃,中午又上升了3℃,下午有雨冷空气南下,到夜间又下降了9℃,则这天夜间的温度是℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
相关试题

