【题目】下列计算中,不正确的有( )
①(ab2)3=ab6;②(3xy2)3=9x3y6;③(﹣2x3)2=﹣4x6;④(﹣a2m)3=a6m.
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
根据整数指数幂的运算法则进行计算并做出判断即可.
解:①(ab2)3=a2b6,故①错误;
②(3xy2)3=27x3y6,故②错误;
③(-2x3)2=4x6,故③错误;
④(-a2m)3=-a6m,故④错误.
所以不正确的有4个.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x3)4的结果是( )
A. x7 B. x12 C. x81 D. x64
-
科目: 来源: 题型:
查看答案和解析>>【题目】AC是ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
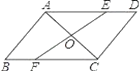
(1)求证:AE=CF;
(2)连接AF,CE.
①当EF和AC满足条件 时,四边形AFCE是菱形;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,EF的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中点D、E分别在边AC、AB上,BD和CE相交于点O,有下面三个条件:①∠EBO=∠DCO,②BE=CD,③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定出AB=AC.
(2)选择(1)中的一种情形,写出证明的过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x|=4,|y|=1,且xy<0,则x﹣y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
相关试题

