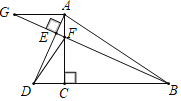
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=![]() ,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;
(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);
(3)如果AG=8,求DE的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)求出AC=3,可得∠DAC=∠FBC,则tan∠FBC=tan∠DAC=![]() ;
;
(2)由条件可得∠AGF=∠CBF,可得![]() ,可用x表示CF和AF的长,求出CD,则S△DAF=
,可用x表示CF和AF的长,求出CD,则S△DAF=![]() ,可用x表示结果;
,可用x表示结果;
(3)分两种情况,①当点D在BC的延长线上时,②当点D在BC的边上时,可求出AE长AD的长,则DE=AD﹣AE可求出.
解:
(1)∵∠ACB=90![]() ,BC=4,sin∠ABC=
,BC=4,sin∠ABC=![]() ,
,
∴设AC=3x,AB=5x,
∴(3x)2+16=(5x)2,
∴x=1,
即AC=3,
∵BE⊥AD,
∴∠AEF=90![]() ,
,
∵∠AFE=∠CFB,
∴∠DAC=∠FBC,
∴tan∠FBC=tan∠DAC=![]() ;
;
(2)∵AG∥BD,
∴∠AGF=∠CBF,
∴tan∠AGF=tan∠CBF,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠EAF=∠CBF,
∴![]() ,
,
∴![]() ,
,
∴S△DAF=![]() ;
;
(3)①当点D在BC的延长线上时,如图1,
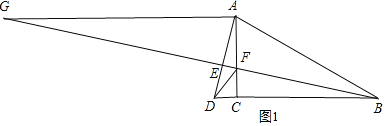
∵AG=8,BC=4,AG∥BD,
∴![]() ,
,
∴AF=2CF,
∵AC=3,
∴AF=2,CF=1,
∴![]() ,
,
∴![]() ,
,
设AE=x,GE=4x,
∴x2+16x2=82,
解得x=![]() ,
,
即AE=![]() ,
,
同理tan∠DAC=tan∠CBF,
∴![]() ,
,
∴DC=![]() ,
,
∴AD=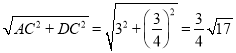 ,
,
∴![]() ,
,
②当点D在BC的边上时,如图2,
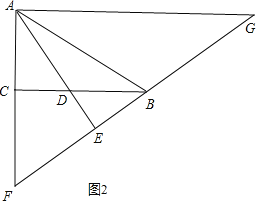
∵AG∥BD,AG=8,BC=4,
∴![]() ,
,
∴AF=6,
∵∠EAF=∠CBF=∠ABC,
∴cos∠EAF=cos∠ABC,
∴![]() ,
,
∴![]() ,
,
同理![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴DE=AE﹣AD=![]() ,
,
综合以上可得DE的长为![]() 或
或![]() ;
;

