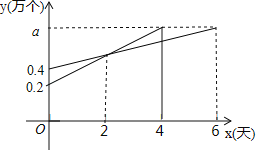
【题目】为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于 万个.
参考答案:
【答案】1
【解析】
试题分析:结合函数图象,设乙企业每天生产足球x万个,则甲企业每天生产足球2x万个,根据企业供应的足球数=库存+每日产量×生产天数,得出关于x、a的二元一次方程组,解方程组即可得出结论.
解:∵(6﹣2)÷(4﹣2)=2,
∴设乙企业每天生产足球x万个,则甲企业每天生产足球2x万个,
根据题意可得:![]() ,
,
解得:![]() .
.
∴每家企业供应的足球数量a=1万个.
故答案为:1.
-
科目: 来源: 题型:
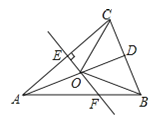
查看答案和解析>>【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
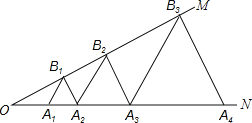
A.6 B.12 C.32 D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
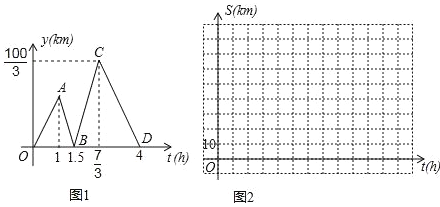
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过
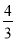 h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和是720°,那么这个多边形是( )
A.四边形
B.五边形
C.六边形
D.七边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的两边长分别是2和5,则第三边可能是( )
A.2 B.3 C.5 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁从数轴上A点出发爬了4个单位长度到了表示1的点B,则点A所表示的数是( )
A. 3或5 B. 5或3 C. 5 D. 3
相关试题

