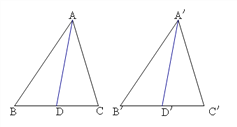
【题目】如图,△ABC≌△A'B'C',AD、A'D'分别是△ABC、△A'B'C'的对应边上的中线,判断AD与A'D'有怎样的数量关系?证明你的结论.
参考答案:
【答案】AD=A'D',证明见解析.
【解析】试题分析:先由全等三角形的性质得出AB=A'B',BC=B'C',∠B=∠B',再 由中线的性质得出BD=B'D',最后由SAS证出△ABD≌△A'B'D',即可得出AD=A'D'.
试题解析:AD=A'D',证明如下:
证明: ∵△ABC≌△A'B'C',
∴AB=A'B',BC=B'C',∠B=∠B',
∵AD、A'D'分别是BC与B'C'边上的中线,
∴BD=B'D',
在△ABD和△A'B'D'中,
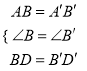 ,
,
∴△ABD≌△A'B'D'(SAS),
∴ AD=A'D'.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市八年级学生体重,对该市1000名八年级学生的体重进行抽样调查.你知道这个例子中的样本是__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个角为50°,则另两个角的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的每个外角等于60°,则这个正多边形是( )
A.正五边形
B.正六边形
C.正七边形
D.正八边形 -
科目: 来源: 题型:
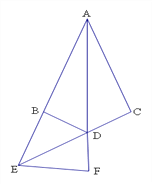
查看答案和解析>>【题目】如图,AB=AC,DB=DC,
(1)求证:AD平分∠BAC;
(2)延长CD与AB的延长线交于E ,延长AD到F,使DF=DC,连接EF,若∠C=100°,∠BAC=40°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+2%表示增加2%,那么﹣6%表示( )
A.增加14%
B.增加6%
C.减少26%
D.减少6% -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
相关试题

