【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD平分∠BAC;②作图依据是S.A.S;③∠ADC=60°; ④点D在AB的垂直平分线上
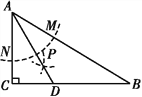
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】①根据作图的过程可以判定AD是∠BAC的∠平分线;
②根据作图的过程可以判定出AD的依据;
③利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质求∠ADC的度数;
④利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点在AB的中垂线上.
解:如图所示,
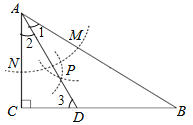
①根据作图的过程可知,AD是∠BAC的∠平分线;
故①正确;
②根据作图的过程可知,作出AD的依据是SSS;
故②错误;
③∵在△ABC中,∠C=90°,∠B=30°,
∴∠CBA=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°-∠2=60°,即∠ADC=60°.
故③正确;
④∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故④正确;
故选C.
“点睛”此题主要考查的是作图-基本作图,涉及到角平分线的作法以及垂直平分线的性质,熟练根据角平分线的性质得出∠ADC的度数是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016重庆市第20题)某校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校1600名学生每人都参加且只参加了其中一个社团的活动,校团委从这1600名学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如下不完整的统计图,请根据统计图完成下列问题:
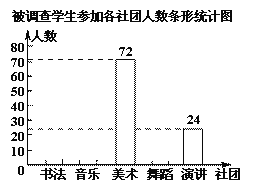

参加本次调查有_____名学生,根据调查数据分析,全校约有______名学生参加了音乐社团;请你补全条形统计图。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年,宜宾市有5481000人口,将5481000用科学计数法(保留两个有效数字)表示为( )
A. 54×105 B. 0.55×106 C. 5.5×106 D. 5.4×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张正方形纸片,第1次剪成四个大小形状一样的小正方形,第2次将其中的一个小正方形再按同样的方法剪成四个小正方形,然后再将其中的一个小正方形剪成四个小正方形,如此循环进行下去,如果共剪
 次,则可剪出 个正方形.
次,则可剪出 个正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB为锐角,点D为BC边上一动点,连接AD,以AD为直角边且在AD的上方作等腰直角三角形ADF.
(1)如图1,若AB=AC,∠BAC=90°,当点D在线段BC上时(不与点B重合),
证明:△ACF≌△ABD
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,猜想CF与BD的数量关系和位置关系是什么,并说明理由;
(3)如图3,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动(不与点B重合),试探究CF与BD位置关系.



-
科目: 来源: 题型:
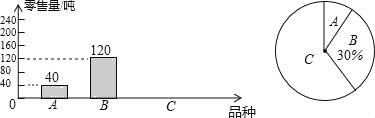
查看答案和解析>>【题目】(2016广东省茂名市第19题)为了解茂名某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空
(1)等边三角形是轴对称图形,它有条对称轴;
(2)等边三角形的每个内角都等于;条边上都“三线合一”.
相关试题

