【题目】如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是 ;若∠BED=50°,则∠C的度数是 .
(2)探究∠BED与∠C的数量关系,并证明你的结论.

参考答案:
【答案】(1)55°,80°;(2)∠BED=90°﹣![]() ∠C
∠C
【解析】
(1)根据三角形的内角和得到∠ABC=50°,根据角平分线的定义得到∠CAD=![]() ∠BAC=30°,∠DBE=
∠BAC=30°,∠DBE=![]() ∠ABC=25°,根据三角形的内角和即可得到结论;
∠ABC=25°,根据三角形的内角和即可得到结论;
(2)根据角平分线的定义和三角形的内角和即可得到结论.
(1)∵∠C=70°,∠BAC=60°,
∴∠ABC=50°,
∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠CAD=![]() ∠BAC=30°,∠DBE=
∠BAC=30°,∠DBE=![]() ∠ABC=25°,
∠ABC=25°,
∵∠ADB=∠DAC+∠C=100°,
∴∠BED=180°﹣100°﹣25°=55°,
∵∠BED=50°,
∴∠ABE+∠BAE=50°,
∴∠ABC+∠BAC=2×50°=100°,
∴∠C=80°;
故答案为:55°,80°;
(2)∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠ABE=![]() ∠ABC,∠BAE=
∠ABC,∠BAE=![]() ∠BAC,
∠BAC,
∵∠BED=∠ABE+∠BAE=![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)=![]() (180°﹣∠C)=90°﹣
(180°﹣∠C)=90°﹣![]() ∠C.
∠C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
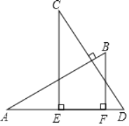
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
-
科目: 来源: 题型:
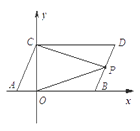
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-2,0),(6,0),现同时将点A,B分别向上平移4个单位,再向右平移2个单位,分别得到点A,B的对应点C、D,连接AC、BD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC
(2)在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①
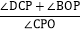 的值不变;②
的值不变;②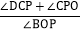 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.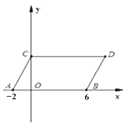
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.

(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B,C分别在AD,AF上,此时BD=CF,BD⊥CF成立.
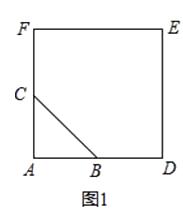
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交AF,CF于点N,H.
①求证:BD⊥CF;
②当AB=2,AD=3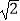 时,求线段AN的长.
时,求线段AN的长.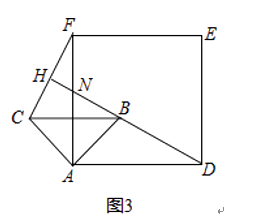
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

相关试题

