【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
求证: (1)△ACD≌△BCE.
(2)△PCQ为等边三角形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析: ![]() 利用
利用![]() 易证得
易证得![]()
![]() 证明
证明![]() 则可得
则可得![]() 又由
又由![]() 即可证得:
即可证得: ![]() 为等边三角形.
为等边三角形.
试题解析:如图,

(1)∵△ABC和△CDE为等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°.
∴∠ACB+∠3=∠ECD+∠3,
即∠ACD=∠BCE.
又∵C在线段AE上,
∴∠3=60°.
在△ACD和△BCE中,

∴△ACD≌△BCE.
(2) ∵△ACD≌△BCE.
∴∠1=∠2.
在△APC和△BQC中,

∴△APC≌△BQC.∴CP=CQ.
∵∠3=60°,CP=CQ..
∴△PCQ为等边三角形(有一个角是60°的等腰三角形是等边三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,正确的是( )
A.a4a4=2a4B.a6÷a3=a2
C.(a﹣b)2=a2﹣b2D.(﹣3a2b)2=9a4b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二元一次方程
 ﹣
﹣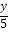 =4
=4
(1)若y的值是非负数,求x的取值范围
(2)已知关于x、y的二元一次方程组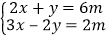 的解满足二元一次方程
的解满足二元一次方程 ﹣
﹣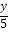 =4 , 求m的值.
=4 , 求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A表示的数是-5 , 点B到点A的距离是3, 则点B所表示的数是________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体中没有曲面的是( )
A. 球 B. 圆柱 C. 棱柱 D. 圆锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么方程3⊕x=13的解为x=_____.
相关试题

