【题目】解方程组
．
【答案】解：
，③＋①得：3x＋5y=11④，③×2＋②得：3x＋3y=9⑤，④－⑤得：2y=2，y=1，将y=1代入⑤得：3x=6，x=2，将x=2，y=1代入①得：z=6－2×2－3×1=－1，∴方程组的解为：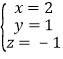
【解析】解方程组 ，③＋①得：3x＋5y=11④，③×2＋②得：3x＋3y=9⑤，④－⑤得：2y=2，y=1，将y=1代入⑤得：3x=6，x=2，将x=2，y=1代入①得：z=6－2×2－3×1=－1，∴方程组的解为：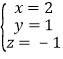
【考点精析】解答此题的关键在于理解解三元一次方程组的相关知识，掌握通过“代入”或“加减”消元，把“三元”化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而转化为解一元一次方程．
科目：初中数学 来源： 题型：
【题目】如图1，在正方形ABCD中，点P为AD延长线上一点，连接AC、CP，过点C作CF⊥CP于点C，交AB于点F，过点B作BM⊥CF于点N，交AC于点M．
（1）若
， 
，求
；
（2）若
，求证： 
；
（3）如图2，在其他条件不变的情况下，将“正方形ABCD”改为“矩形ABCD”，且 AB≠BC，AC=AP，取CP中点E，连接EB，交AC于点O，猜想：∠AOB与∠ABM之间有何数量关系？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠A=100°，BI、CI分别平分∠ABC，∠ACB，则∠BIC=________，若BM、CM分别平分∠ABC，∠ACB的外角平分线，则∠M=__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】纳米是非常小的长度单位，1纳米=10﹣9米．某种病菌的长度约为50纳米，用科学记数法表示该病菌的长度，结果正确的是（ ）
A.5×10﹣10米B.5×10﹣9米C.5×10﹣8米D.5×10﹣7米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请将下列事件发生的概率标在图中：
（1）随意掷两枚质地均匀的骰子，朝上面的点数之和为1；
（2）抛出的篮球会下落；
（3）从装有3个红球、7个白球的口袋中任取一个球，恰好是红球（这些球除颜色外完全相同）；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1：y＝x+1与直线l2：y＝mx+n相交于点P（1，b）．①求b的值；②不解关于x ， y的方程组 
，请你直接写出它的解；
③直线l3：y=nx+m是否也经过点P？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com