【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
参考答案:
【答案】
(1)解:设每千克应涨价x元,则(10+x)(500﹣20x)=6 000
解得x=5或x=10,
为了使顾客得到实惠,所以x=5
答:要保证每天盈利6000元,同时又使顾客得到实惠,那么每千克应涨价5元
(2)解:设涨价z元时总利润为y,
则y=(10+z)(500﹣20z)
=﹣20z2+300z+5 000
=﹣20(z2﹣15z)+5000
=﹣20(z2﹣15z+ ![]() ﹣
﹣ ![]() )+5000
)+5000
=﹣20(z﹣7.5)2+6125
当z=7.5时,y取得最大值,最大值为6 125
答:若该商场单纯从经济角度看,每千克这种水果涨价7.5元,能使商场获利最多
【解析】本题的关键是根据题意列出一元二次方程,再求其最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:
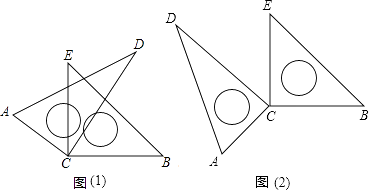
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE等于多少?若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.

(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.两队合作施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划修建一座既是中心对称图形,又是轴对称图形的花坛,从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案,你认为符合条件的是
A.正三角形 B.正五边形 C.等腰梯形 D.菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记算器计算锐角α的三角函数值时,不能直接计算出来的三角函数值是( )
A.cotα
B.tanα
C.cosα
D.sinα -
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意正整数n,按照n→平方→+n→÷n→﹣n→答案程序计算,应输出的答案是( )
A.n2﹣n+1 B.n2﹣n C.3﹣n D.1
-
科目: 来源: 题型:
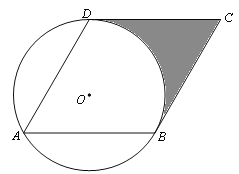
查看答案和解析>>【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
相关试题

