【题目】如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
设B′C′与AB交点为D,根据等腰直角三角形的性质求出∠BAC=45°,再根据旋转的性质求出∠CAC′=15°,AC′=AC,然后求出∠C′AD=30°,再根据直角三角形30°角所得到直角边等于斜边的一半可得AD=2C′D,然后利用勾股定理列式求出C′D,再利用三角形的面积公式列式进行计算即可得解.
如图,设B′C′与AB交点为D,
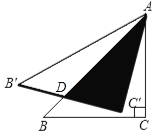
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵△AB′C′是△ABC绕点A逆时针旋转15°后得到,
∴∠CAC′=15°,AC′=AC=1,
∴∠C′AD=∠BAC﹣∠CAC′=45°﹣15°=30°,
∵AD=2C′D,
∴AD2=AC′2+C′D2,
即(2C′D)2=12+C′D2,
解得C′D=![]() ,
,
故阴影部分的面积=![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.
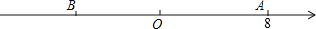
(1)写出数轴上点B表示的数;
(2)若点M、N分别是线段AO、BO的中点,求线段MN的长;
(3)若动点P从点A出发.以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.问点P运动多少秒时追上点Q?
-
科目: 来源: 题型:
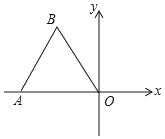
查看答案和解析>>【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,画出△OA′B′,写出点A′,B′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:
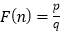 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有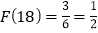 .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)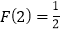 ;(2)
;(2)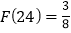 ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2 , 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 , 以此类推…则正方形OB2016B2017C2017的顶点B2017的坐标是( )
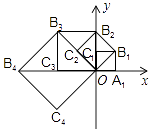
A.(21008 , 0)
B.(21008 , 21008)
C.(0,21008)
D.(21007 , 21007) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=3∠B,AB=10,AC=4,AD平分∠BAC,交BC于点D,CE⊥AD于E,则CE= ______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,

(1)求证:△ABE≌△BCD;
(2)求出∠AFB的度数.
相关试题

