【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 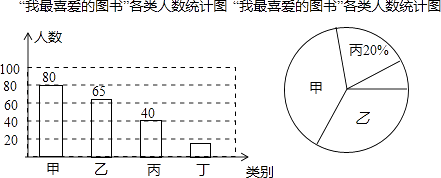
请你结合图中信息,解答下列问题(其中(1)、(2)直接填答案即可):
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生2000人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
参考答案:
【答案】
(1)200
(2)15;40
(3)解:设该校最喜爱丙类图书的女生和男生分别1.5x人,x人,
根据题意列出方程得:x+1.5x=2000×20%,
解得:x=160,
此时1.5x=240,
则该校最喜爱丙类图书的女生和男生分别为240人,160人
【解析】解:(1)根据题意得:40÷20%=200(名),
故答案为:200;(2)根据题意得:丁类学生数为200﹣(80+65+40)=15(名);
最喜爱甲类图书的人数占本次被调查人数的百分比= ![]() ×100%=40%;
×100%=40%;
故答案为:15,40;
(1)根据丙对应的人数以及百分比,即可得到调查的人数;(2)根据200﹣(80+65+40)进行计算,即可得到喜爱丁类图书的学生人数,根据喜爱甲类图书的人数除以总人数,即可得到最喜爱甲类图书的人数占本次被调查人数的百分数;(3)设该校最喜爱丙类图书的女生和男生分别1.5x人,x人,再根据题意列出方程得:x+1.5x=2000×20%,进而得到该校最喜爱丙类图书的女生和男生的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a2﹣9的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是 .
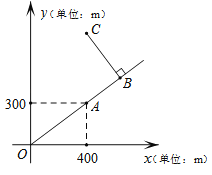
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而菱形不具有的性质是( )
A.两组对边分别平行B.对角线互相垂直
C.对角线相等D.两组对角分别相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
220
180
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】意大利著名画家达芬奇验证勾股定理的方法如下:
①在一张长方形的纸板上画两个边长分别为a、b的正方形,并连接BC、FE.
②沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ,请动手做一做.
③将纸板Ⅱ翻转后与Ⅰ拼成其他的图形.
④比较两个多边形ABCDEF和A′B′C′D′E′F′的面积,你能验证勾股定理吗?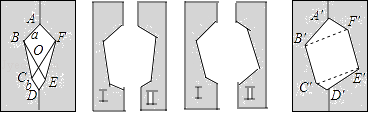
相关试题

