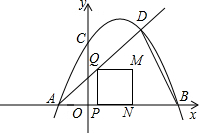
（2012•景宁县模拟）已知二次函数y=-x2+4x+5图象交x轴于点A、B，交y轴于点C，点D是该函数图象上一点，且点D的横坐标为4，连BD，点P是AB上一动点（不与点A重合），过P作PQ⊥AB交射线AD于点Q，以PQ为一边在PQ的右侧作正方形PQMN．设点P的坐标为（t，0）．
（1）求点B，C，D的坐标及射线AD的解析式；
（2）在AB上是否存在点P，使△OCM为等腰三角形？若存在，求正方形PQMN 的边长；若不存在，请说明理由；
（3）设正方形PQMN与△ABD重叠部分面积为s，求s与t的函数关系式．
分析：（1）根据二次函数解析式，当x=0时，求出C点坐标；当y=0时，求出B点坐标及点A坐标；将D点横坐标代入y=-x2+4x+5，即可求出点D纵坐标；根据点A、点D坐标，应用待定系数法即可求出射线AD解析式；
（2）假设存在点P，使△OCM为等腰三角形，根据勾股定理，若能求出P点坐标，则P存在，同时可求出正方形PQMN 的边长；否则P不存在；
（3）由于重叠部分面积是不确定的，所以要根据其重叠程度，分情况讨论，得到不同的表达式．
解答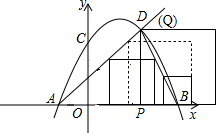：解：（1）当x=0时，y=5，则C点坐标为（0，5），
当y=0时，-x2+4x+5=0，
解得（x+1）（x-5）=0，
x1=-1；x2=5．
则A点坐标为（-1，0），B点坐标为（5，0）．
将x=4代入y=-x2+4x+5得，y=-16+16+5=5，
则D点坐标为（4，5）．
设AD的解析式为y=kx+b，
把A（-1，0），D（4，5）分别代入解析式y=kx+b得，
-k+b=0
4k+b=5
，
解得
k=1
b=1
，
函数解析式为y=x+1（x≥-1）．（2分）

（2）∵直线AD的解析式为：y=x+1，且P（t，0）．
∴Q（t，t+1），M（2t+1，t+1）
当MC=MO时：t+1=
5
2
，
∴边长为
5
2
．…（1分）
当OC=OM时：（2t+1）2+（t+1）2=52
解得t1=-
3
5
-
2
31
5
（舍去），t1=-
3
5
+
2
31
5

∴边长为t+1=
2
5
+
2
31
5
．…（2分）
当CO=CM时：（2t+1）2+（4-t）2=52
解得t1=
2+2
11
5
，t2=
2-2
11
5
．
∴边长为t+1=
7+2
11
5
．
或t+1=t2=
7-2
11
5
…（2分）

（3）当1＜t≤
19
11
时，正方形的边长为（t+1），故其面积为：s=（t+1）2；…（1分）
当
19
11
≤t≤2时：s=-
111
10
t2+
219
5
t-
351
5
；…（1分）
当2≤t≤4时：s=-
11
10
t2+
19
5
t+
49
10
；…（1分）
当4≤t≤5时：s=
5
2
t2-25t+
125
2
．…（1分）
点评：本题考查了二次函数的图象和性质、待定系数法求一次函数解析式、三角形及正方形的性质、存在性问题等内容，综合性强，属于难题．
关闭