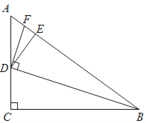
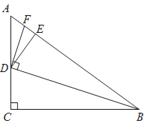
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
参考答案:
【答案】(1)证明见解析;(2)AD2=AF·AB,理由见解析;(3)5+2![]() .
.
【解析】试题解析:(1)根据题意得∠ADF+∠BDC=∠EDF+∠BDE=90°,由折叠可知,∠BDE=∠BDC.所以∠ADF=∠EDF;
(2)易证△ADF∽△ABD,得AF∶AD=AD∶AB=DF∶DB,得AD2=AF·AB;
(3)设AE=x,DE=![]() x,由勾股定理可得,AD=DE=
x,由勾股定理可得,AD=DE=![]() x,可证△ADE∽△DFE,得BE=2x2,由(2)知AD2=AF·AB,即3x2=(x-1)×(x+2x2).解得x 的值,即可求BC的值
x,可证△ADE∽△DFE,得BE=2x2,由(2)知AD2=AF·AB,即3x2=(x-1)×(x+2x2).解得x 的值,即可求BC的值
试题解析:(1)∵DF⊥DB,∴∠BDF=90°.
∴∠ADF+∠BDC=∠EDF+∠BDE=90°
由折叠可知,∠BDE=∠BDC.
∴∠ADF=∠EDF.
(2)AD,AF,AB之间的数量关系为AD2=AF·AB,理由如下:
由折叠可知,∠DEF=∠BFD=∠C=90°.
∴∠EDF+∠DFE=∠ABD+∠DFE=90°.
∴∠EDF=∠ABD.
∴∠ADF=∠DBA.
∵∠A=∠A,∴△ADF∽△ABD.
∴AF∶AD=AD∶AB=DF∶DB.
∴AD2=AF·AB.
(3)在Rt△ADE中,tanA=DE∶AE=![]() ∶1,则可设AE=x,DE=
∶1,则可设AE=x,DE=![]() x,由勾股定理可得,AD=DE=
x,由勾股定理可得,AD=DE=![]() x.
x.
∵∠ABD=∠EDF,∠AED=∠DEF,
∴△ADE∽△DFE. ∴DE∶EF=BE∶DE,即DE2=EF·EB.
∴(![]() x)2=1×BE,即BE=2x2。
x)2=1×BE,即BE=2x2。
由(2)知AD2=AF·AB,
∴(![]() x)2=(AE-EF)(AE+BE)=(x-1)×(x+2x2).
x)2=(AE-EF)(AE+BE)=(x-1)×(x+2x2).
即3x2=(x-1)×(x+2x2).
解得,x=1+![]() ,x=1-
,x=1-![]() (舍).
(舍).
∴BE=2x2=2(1+![]() )2=5+2
)2=5+2![]() .
.
由折叠可知,BC=BE=5+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.
(1)写出两个不全等且与△GHC相似的三角形,并任选其中的一个进行证明;
(2)求GH的长.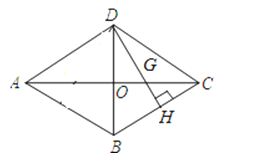
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABO中,AB⊥OB,OB=
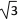 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为____.
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为____.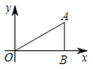
-
科目: 来源: 题型:
查看答案和解析>>【题目】同一平面内,两条不重合的直线的位置关系是( )
A. 平行或垂直 B. 平行或相交 C. 平行、相交或垂直 D. 相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类且定价为15元的图书.书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠,学校如果多买12本,则可以享受优惠且所花钱数与原来相同,问学校获奖的同学有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形对应边之比是1:4,那么它们的对应高线之比是( )
A.1:4B.1:6C.1:8D.1:16
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x+y=4的解是( )
A.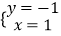
B.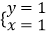
C.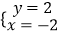
D.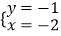
相关试题

