【题目】点O是直线AB上一点,∠COD是直角,OE平分∠BOC.
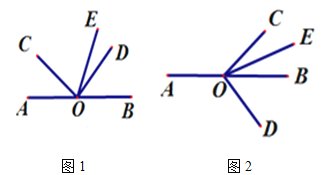
(1)①、如图1,若∠AOC=50°,求∠DOE的度数;
②、如图1,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(2)将图1中的∠COD按顺时针方向旋转至图2所示的位置.
探究∠AOC与∠DOE的度数之间的关系,写出你的结论,并说明理由.
参考答案:
【答案】(1)①、20°;②、∠DOE=![]() α;(2)∠DOE=
α;(2)∠DOE=![]() ∠AOC;理由见解析.
∠AOC;理由见解析.
【解析】
试题分析:(1)①首先根据180°-∠AOC求出∠BOC的度数,根据角平分线的性质的性质得出∠COE的度数,然后根据∠DOE=∠COD-∠COE得出答案;②、根据①得出规律;(2)根据题意得出∠BOC=180°-∠AOC,根据角平分线的性质得出∠COE=90°-![]() ∠AOC,最后根据∠DOE=∠COD-∠COE得出答案.
∠AOC,最后根据∠DOE=∠COD-∠COE得出答案.
试题解析:(1)①∵∠BOC=180°-∠AOC=180°-40°=140° 又∵OE平分∠BOC
∴∠COE=![]() ∠BOC=
∠BOC=![]() ×140°=70° ∴∠DOE=∠COD-∠COE=90°-70°=20°
×140°=70° ∴∠DOE=∠COD-∠COE=90°-70°=20°
②、∠DOE=![]() α
α
、∠DOE=![]() ∠AOC
∠AOC
理由如下:∵∠BOC=180°-∠AOC OE平分∠BOC
∴∠COE=![]() ∠BOC=
∠BOC=![]() ×(180°-∠AOC)=90°-
×(180°-∠AOC)=90°-![]() ∠AOC
∠AOC
∴∠DOE=∠COD-∠COE=90°-(90°-![]() ∠AOC)=
∠AOC)=![]() ∠AOC
∠AOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.

(1)求证:△ABC∽A′B′C′;
(2)A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求画图,并回答问题.
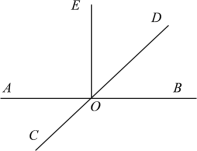
已知:直线AB,CD相交于点O,且OE⊥AB.
(1)过点O画直线MN⊥CD;
(2)若点F是(1)中所画直线MN上任意一点(O点除外),若∠AOC=35°,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_______处.

-
科目: 来源: 题型:
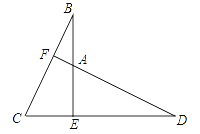
查看答案和解析>>【题目】已知:如图,BE⊥CD,BE=DE,BC=DA.
求证:(1)△BEC≌△DAE;
(2)DF⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=135°,AD⊥BC于D,且AB+BD=DC,那么∠C= °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A,B对应的数分别为-4,8.
(1)如图1,如果点P和点Q分别从点A,点B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
① 求A,B两点之间的距离.
② 当P,Q两点相遇时,点P在数轴上对应的数几.
③ 求点P出发多少秒后,与点Q之间相距4个单位长度?
(2)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?


相关试题

