【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
参考答案:
【答案】解:过点A作AH⊥CD,垂足为H,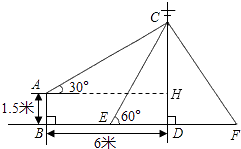
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH= ![]() ,
,
∴CH=AHtan∠CAH,
∴CH=AHtan∠CAH=6tan30°=6× ![]() (米),
(米),
∵DH=1.5,
∴CD=2 ![]() +1.5,
+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED= ![]() ,
,
∴CE= ![]() =4+
=4+ ![]() ≈5.7(米),
≈5.7(米),
答:拉线CE的长约为5.7米.
【解析】由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
-
科目: 来源: 题型:
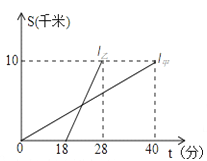
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达;
②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲;
④乙出发6分钟后追上甲.
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若5x = 4x –7,那么5x– __________= –7,变形依据是 ____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
 ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年,新疆某次足球联赛规定每队胜一场得3分,平一场得1分,负一场得0分,某队前14场保持不败,共得32分,设该队平了x场,根据题意列方程得:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题:
为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A
B
价格(万元/台)
a
b
节省的油量(万升/年)
2.4
2
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.

(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
相关试题

