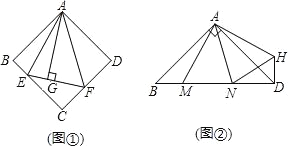
【题目】(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN2,ND2,DH2之间的数量关系,并说明理由.
(3)在图①中,若EG=4,GF=6,求正方形ABCD的边长.
参考答案:
【答案】(1) 45°.(2) MN2=ND2+DH2.理由见解析;(3)12.
【解析】
试题分析:(1)先根据AG⊥EF得出△ABE和△AGE是直角三角形,再根据HL定理得出△ABE≌△AGE,故可得出∠BAE=∠GAE,同理可得出∠GAF=∠DAF,由此可得出结论;
(2)由旋转的性质得出∠BAM=∠DAH,再根据SAS定理得出△AMN≌△AHN,故可得出MN=HN.再由∠BAD=90°,AB=AD可知∠ABD=∠ADB=45°,根据勾股定理即可得出结论;
(3)设正方形ABCD的边长为x,则CE=x-4,CF=x-6,再根据勾股定理即可得出x的值.
试题解析:(1)在正方形ABCD中,∠B=∠D=90°,
∵AG⊥EF,
∴△ABE和△AGE是直角三角形.
在Rt△ABE和Rt△AGE中,
![]() ,
,
∴△ABE≌△AGE(HL),
∴∠BAE=∠GAE.
同理,∠GAF=∠DAF.
∴∠EAF=∠EAG+∠FAG=![]() ∠BAD=45°.
∠BAD=45°.
(2)MN2=ND2+DH2.
由旋转可知:∠BAM=∠DAH,
∵∠BAM+∠DAN=45°,
∴∠HAN=∠DAH+∠DAN=45°.
∴∠HAN=∠MAN.
在△AMN与△AHN中,
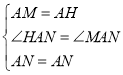 ,
,
∴△AMN≌△AHN(SAS),
∴MN=HN.
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°.
∴∠HDN=∠HDA+∠ADB=90°.
∴NH2=ND2+DH2.
∴MN2=ND2+DH2.
(3)由(1)知,BE=EG=4,DF=FG=6.
设正方形ABCD的边长为x,则CE=x-4,CF=x-6.
∵CE2+CF2=EF2,
∴(x-4)2+(x-6)2=102.
解这个方程,得x1=12,x2=-2(不合题意,舍去).
∴正方形ABCD的边长为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣1)×(﹣2)的结果是( )
A. 2 B. 1 C. ﹣2 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:
 =1.73,
=1.73, =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.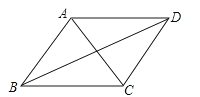
A.①③
B.②③
C.③④
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣a)2a3的结果是( )
A.a5
B.a6
C.﹣a5
D.﹣a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行),某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式
直接销售
粗加工后销售
精加工后销售
每吨获利(元)
100
250
450
(1)现在该公司收购了140吨蔬菜,如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:销售方式
全部直接销售
全部粗加工后销售
尽量精加工,剩余部分直接销售
获利(元)
(2)如果先进行精加工,然后进行粗加工,要求15天刚好加工完140吨蔬菜,则应如何分配加工时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=36x2的叙述,错误的是( )
A.图象的对称轴是y轴
B.图象的顶点是原点
C.当x>0时,y随x的增大而增大
D.y有最大值
相关试题

