【题目】如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.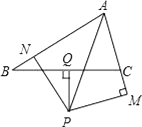
参考答案:
【答案】解:BN=CM,理由如下:
如图,连接PB,PC,
∵AP是∠BAC的平分线,PN⊥AB,PM⊥AC,
∴PM=PN,∠PMC=∠PNB=90°,
∵P在BC的垂直平分线上,
∴PC=PB,
在Rt△PMC和Rt△PNB中, ![]() ,
,
∴Rt△PMC≌Rt△PNB(HL),
∴BN=CM.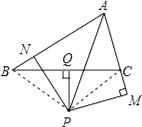
【解析】连接PB,PC,根据角平分线性质求出PM=PN,根据线段垂直平分线求出PB=PC,根据HL证Rt△PMC≌Rt△PNB,即可得出答案.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中最适合使用普查方式收集数据的是( )
A.为制作校服,了解某班同学的身高情况
B.了解全市初三学生的视力情况
C.了解一种节能灯的使用寿命
D.了解我省农民的年人均收入情况 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个纸盒里装有四张除数字以外完全相同卡片,四张卡片上的数字分别为1,2,3,4.先从纸盒里随机取出一张,记下数字为
 ,再从剩下的三张中随机取出一张,记下数字为
,再从剩下的三张中随机取出一张,记下数字为 ,这样确定了点P的坐标(
,这样确定了点P的坐标( ,
,  ).
).(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(
 ,
,  )在函数
)在函数 =-
=-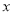 +4图象上的概率.
+4图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个数中,与4互为相反数的是( )
A. ﹣22 B. (﹣2)2 C. ﹣(﹣4) D. (﹣1)4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
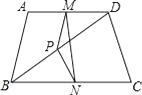
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数是a,在它的左边加上一个数字b变成一个三位数,则这个三位数用代数式表示为( )
A. 10a+100b B. ba C. 100ba D. 100b+a
-
科目: 来源: 题型:
查看答案和解析>>【题目】若有理数a、b满足:|a+2|+|b﹣2|=0,求(a+b)﹣ab的值.
相关试题

