【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.

参考答案:
【答案】(1)证明见解析;(2) 2cm.
【解析】试题分析:(1)根据同角的余角相等可得∠BCE=∠CAD,再由全等三角形的判定定理AAS即可判定△ADC≌△CEB;(2)利用(1)中的全等三角形的对应边相等得到:AD=CE=5cm,CD=BE.则根据图中相关线段的和差关系得到BE=AD-DE,即可求得BE的长度.
试题解析:(1)证明:如图,∵AD⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中,
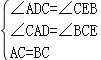 ,
,
∴△ADC≌△CEB(AAS);
(2)由(1)知,△ADC≌△CEB,则AD=CE=5cm,CD=BE.
如图,∵CD=CE﹣DE,
∴BE=AD﹣DE=5﹣3=2(cm),即BE的长度是2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(5分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):

⑴根据记录可知前三天共生产________辆;
⑵产量最多的一天比产量最少的一天多生产________辆;
⑶该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定中小学生每天在校体育活动时间不低于1小时,为此某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生,根据调查结果绘制成的统计图(部分)如图所示:

请根据上述信息解答下列问题:
①请补全统计图;
②本次调查数据的中位数在 组内;
③该辖区约有24000名初中学生,请你估计达到国家规定体育活动时间的人有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个连续的奇数的和是39,则其中最大的奇数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣6>0的解集是( )
A.x>1
B.x<﹣3
C.x>3
D.x<3 -
科目: 来源: 题型:
查看答案和解析>>【题目】“x的2倍与3的差不大于8”列出的不等式是( )
A.2x﹣3≤8
B.2x﹣3≥8
C.2x﹣3<8
D.2x﹣3>8 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方体的长为2×103cm,宽为1.5×102cm,高为1.2×102cm,则它的体积是 ______ cm3.
相关试题

