【题目】已知:如图,在□ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
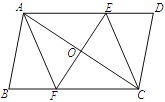
(1)求证:△AOE≌△COF;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是 (直接写出这个条件).
参考答案:
【答案】(1)证明见解析;(2)EF⊥AC.
【解析】
试题分析:此题主要考查了平行四边形的性质,以及全等三角形的判定和性质,关键是掌握平行四边形的对边相等;平行四边形的对角相等.
(1)首先根据平行四边形的性质可得AB=CD,∠B=∠D,AD=BC,AD∥BC,然后证明△AOE≌△COF,可得CF=AE,再证明DE=BF,进而可证明△ABF≌△CDE;
(2)在证明△AOE≌△COF的过程中,只需要∠AOE=∠FOC,对顶角相等即可,无需垂直,因此EF⊥AC是多余条件.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO,
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF;
(2)EF⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB=CD,要使四边形ABCD是中心对称图形,只需添加一个条件,这个条件可以是 ▲ .(只要填写一种情况)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=-x2向左平移1个单位长度,然后向上平移3个单位长度,则平移后抛物线的解析式为( )
A. y=-(x-1)-3 B. y=-(x+1)-3
C. y=-(x-1)+3 D. y=-(x+1)+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】把分别标有数字2、3、4、5的四个小球放入A袋内,把分别标有数字
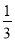 、
、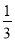 、
、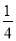 、
、 、
、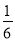 的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明.
的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明.(1)小明分别从A、B两个袋子中各摸出一个小球,求这两个小球上的数字互为倒数的概率。(利用“画树状图”或“列表”的方式给出分析过程)
(2)当B袋中标有
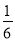 的小球上的数字变为 时(填写所有结果),(1)中的概率为
的小球上的数字变为 时(填写所有结果),(1)中的概率为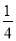 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个多边形:①正三角形;②正方形;③正五边形;④正六边形.其中,既是轴对称图形又是中心对称图形的是( ).
A.①② B.②④ C.②③ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2-2x-1=0时,配方后得的方程为( )
A. (x+1)2=0 B. (x-1)2=0 C. (x+1)2=2 D. (x-1)2=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式4(1-x)>2-3x的非负整数解的个数是( )
A. 3个 B. 2个 C. 1个 D. 0个
相关试题

